
【题目】如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
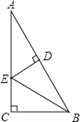
A. 1对 B. 2对 C. 3对 D. 4对
 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】某市有三个景区是人们节假日游玩的热点景区,某学校对七(1)班学生“五一”小长假随父母到这三个景区游玩的计划做了全面调查,调查分四个类别,A:三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩,现根据调查结果绘制了如下不完全的条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)九(1)班现有学生__________人,在扇形统计图中表示“B类别”的扇形的圆心角的度数为__________;
(2)请将条形统计图补充完整;
(3)若该校七年级有1000名学生,求计划“五一”小长假随父母到这三个景区游玩的学生多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
A | B | |
进价(万元/套) | 1.5 | 1.2 |
售价(万元/套) | 1.65 | 1.4 |
该商场计划购进两种教学设备若干套,共需66万元,全部销售后可获毛利润9万元。
(毛利润=(售价 - 进价)×销售量)
(1)该商场计划购进A,B两种品牌的教学设备各多少套?
(2)通过市场调研,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍。若用于购进这两种教学设备的总资金不超过69万元,问A种设备购进数量至多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5月16日,我校进行了全校师生防灾减灾大演练,警报拉响后同学们匀速跑步到操场,在操场指定位置清点人数、听广播后,再沿原路匀速步行回教室,同学们离开教学楼的距离y与时间x的关系的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 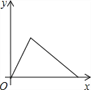
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某剧院的观众席的座位为扇形,且按下列分式设置:
排数(x) | 1 | 2 | 3 | 4 | … |
座位数(y) | 50 | 53 | 56 | 59 | … |
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团参加舞剧《天鹅湖》的表演,已知甲、乙两个团的女演员的身高平均数分别为165cm、165cm,方差分别为S甲2=1.5、S乙2=2.5,则身高更整齐的芭蕾舞团是_____团.
查看答案和解析>>
科目:初中数学 来源: 题型:
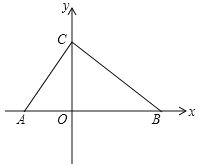
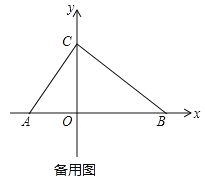
【题目】如图,在平面直角坐标系内,点 O 为坐标原点,点 A 在 x 轴负半轴上,点 B、C 分别在 x 轴、y 轴正半轴上,且 OB=2OA,OB﹣OC=OC﹣OA=2.
(1)求点 C 的坐标;
(2)点 P 从点 A 出发以每秒 1 个单位的速度沿 AB 向点 B 匀速运动,同时点 Q 从点 B 出发 以每秒 3 个单位的速度沿 BA 向终点 A 匀速运动,当点 Q 到达终点 A 时,点 P、Q 均停止运 动,设点 P 运动的时间为 t 秒(t>0),线段 PQ 的长度为 y,用含 t 的式子表示 y,并写出 相应的 t 的范围;
(3)在(2)的条件下,过点 P 作 x 轴的垂线 PM,PM=PQ,是否存在 t 值使点 O 为 PQ 中 点?若存在求 t 值并求出此时三角形 CMQ 的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
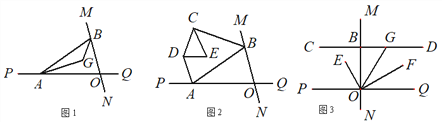
【题目】直线MN与直线PQ相交于O,点A在射线OP上,点B在射线OM上.
(1)如图1,![]() 已知AG、BG分别是∠BAO和∠ABO角的平分线,求
已知AG、BG分别是∠BAO和∠ABO角的平分线,求![]() 的度数;
的度数;
(2)如图2,![]() 已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,∠CED= 度;
已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,∠CED= 度;
(3)如图3,![]() ,过点B作直线CD⊥MN,G为射线BD上一点,OF平分∠QOG,OE⊥OF,探索
,过点B作直线CD⊥MN,G为射线BD上一点,OF平分∠QOG,OE⊥OF,探索![]() 的大小是否发生变化?若不变,求其值;若改变,说明理由.
的大小是否发生变化?若不变,求其值;若改变,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com