
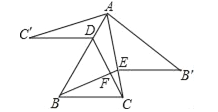
【题目】如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC',△AEB≌△AEB',且C'D∥EB'∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是_____°.(用含x的式子表示)
【答案】![]()
【解析】
延长C′D交AC于M,如图,根据全等的性质得∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,再利用三角形外角性质得∠C′MC=∠C′+∠C′AM=∠C′+2x,接着利用C′D∥B′E得到∠AEB=∠C′MC,而根据三角形内角和得到∠AEB′=180°-∠B′-x,则∠C′+2x=180°-∠B′-x,所以∠C′+∠B′=180°-3x,利用三角形外角性质和等角代换得到∠BFC=∠C=x+∠C′+∠B′,所以∠BFC=180°-2x.
延长C′D交AC于M,如图,

∵△ADC≌△ADC′,△AEB≌△AEB′,∴∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,
∴∠C′MC=∠C′+∠C′AM=∠C′+2x,
∵C′D∥B′E,
∴∠AEB=∠C′MC,
∵∠AEB′=180°∠B′∠B′AE=180°∠B′x,
∴∠C′+2x=180°∠B′x,
∴∠C′+∠B′=180°3x,
∵∠BFC=∠BDF+∠DBF=∠DAC+∠B′=x+∠ACD+∠B′=x+∠C′+∠B′
=x+180°3x=180°2x.
故答案为:![]()


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生体育测试情况,以九年级(1)班学生的体育测试成绩为样本,按A,B,C,D四个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给信息解答下列问题:

(说明:A级:90分~100分;B级:75分~89分;C级:60分~74分;D级:60分以下)
(1)请把条形统计图补充完整;
(2)扇形统计图中D级所在的扇形的圆心角度数是多少?
(3)若该校九年级有600名学生,请用样本估计体育测试中A级学生人数约为多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正整数中,
(1﹣![]() )=(1﹣
)=(1﹣![]() )(1+
)(1+![]() )
)
(1﹣![]() )=(1﹣
)=(1﹣![]() )(1+
)(1+![]() )
)
(1﹣![]() )=(1﹣
)=(1﹣![]() )(1+
)(1+![]() )
)
观察上面的算式,可以归纳得出:![]() = .
= .
利用上述规律,计算下列各式:(1﹣![]() )×(1﹣
)×(1﹣![]() )×(1﹣
)×(1﹣![]() )= .
)= .
(1﹣![]() )×(1﹣
)×(1﹣![]() )×(1﹣
)×(1﹣![]() )×…×(1﹣
)×…×(1﹣![]() )= (请将结题步骤写在下方空白处)
)= (请将结题步骤写在下方空白处)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区将原来400平方米的正方形场地改建成300平方米的长方形场地,且长和宽之比为3∶2.如果把原来正方形场地的铁栅栏围墙利用起来围成新场地的长方形围墙,那么这些铁栅栏是否够用?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个八边形的外角和是°.
B.计划在楼层间修建一个坡角为35°的楼梯,若楼层间高度为2.7m,为了节省成本,现要将楼梯坡角增加11°,则楼梯的斜面长度约减少 m.(用科学计算器计算,结果精确到0.01m)
查看答案和解析>>
科目:初中数学 来源: 题型:
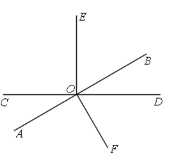
【题目】已知如图,直线AB、CD相交于点O,∠COE=90°,若∠BOD:∠BOC=1:5.
(1)求∠AOC的度数;
(2)如图,过点O作OF⊥AB,求∠DOF与∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;

(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN= ![]() AB,求折痕MN的长;
AB,求折痕MN的长;
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.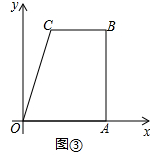
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点,其中A、B两点的坐标分别为(﹣1,0),(0,﹣2),点D在x轴上且AD为⊙M的直径.点E是⊙M与y轴的另一个交点,过劣弧 ![]() 上的点F作FH⊥AD于点H,且FH=1.5
上的点F作FH⊥AD于点H,且FH=1.5
(1)求点D的坐标及该抛物线的表达式;
(2)若点P是x轴上的一个动点,试求出△PEF的周长最小时点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com