
ЁОЬтФПЁПЮЪЬтЬНОПЃК
ЃЈ1ЃЉШчЭМЂйЃЌБпГЄЮЊ4ЕФЕШБпЁїOABЮЛгкЦНУцжБНЧзјБъЯЕжаЃЌНЋЁїOABелЕўЃЌЪЙЕуBТфдкOAЕФжаЕуДІЃЌдђелКлГЄЮЊЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌОиаЮOABCЮЛгкЦНУцжБНЧзјБъЯЕжаЃЌЦфжаOA=8ЃЌAB=6ЃЌНЋОиаЮбиЯпЖЮMNелЕўЃЌЕуBТфдкxжсЩЯЃЌЦфжаAN= ![]() ABЃЌЧѓелКлMNЕФГЄЃЛ
ABЃЌЧѓелКлMNЕФГЄЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌЫФБпаЮOABCЮЛгкЦНУцжБНЧзјБъЯЕжаЃЌЦфжаOA=AB=6ЃЌCB=4ЃЌBCЁЮOAЃЌABЁЭOAгкЕуAЃЌЕуQЃЈ4ЃЌ3ЃЉЮЊЫФБпаЮФкВПвЛЕуЃЌНЋЫФБпаЮелЕўЃЌЪЙЕуBТфдкxжсЩЯЃЌЮЪЪЧЗёДцдкЙ§ЕуQЕФелКлЃЌШєДцдкЃЌЧѓГіелКлГЄЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ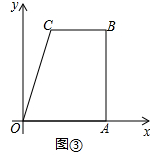
ЁОД№АИЁП
ЃЈ1ЃЉ2
ЃЈ2ЃЉ
НтЃКШчЭМ2жаЃЌBЕФЖдГЦЕуBЁфЃЌелКлЮЊMNЃЌMNНЛBBЁфгкH
ЁпAN= ![]() AB=2ЃЌ
AB=2ЃЌ
ЁрNB=NBЁф=4ЃЌ
дкRtЁїANBЁфжаЃЌABЁф= ![]() =2
=2 ![]() ЃЌ
ЃЌ
ЁрOBЁф=8Љ2 ![]() ЃЌ
ЃЌ
ЁрЕуBЁфЃЈ8Љ2 ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁпBЃЈ8ЃЌ6ЃЉЃЌ
ЁрBBЁфжаЕуHЃЈ8Љ ![]() ЃЌ3ЃЉЃЌЁпЕуNзјБъЃЈ8ЃЌ2ЃЉЃЌ
ЃЌ3ЃЉЃЌЁпЕуNзјБъЃЈ8ЃЌ2ЃЉЃЌ
ЩшжБЯпNHНтЮіЪНЮЊy=kx+bЃЌдђга ![]() НтЕУ
НтЕУ 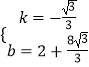 ЃЌ
ЃЌ
ЁржБЯпNHНтЮіЪНЮЊy=Љ ![]() x+2+
x+2+ ![]() ЃЌ
ЃЌ
ЁрЕуMзјБъЃЈ0ЃЌ2+ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрMN= ![]() =
= ![]()
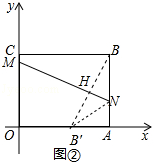
ЃЈ3ЃЉ
НтЃКДцдкЃЎ
РэгЩЃКШчЭМ3жаЃЌбгГЄBQНЛOAгкBЁхЃЌСЌНгAQЃЌЙ§ЕуQзїMNЁЮOAЃЌНЛOCгкMЃЌНЛABгкNЃЎ
ЁпQЃЈ4ЃЌ3ЃЉЃЌ
ЁрNЃЈ6ЃЌ3ЃЉЃЌ
ЁрBN=ANЃЎQB=QBЁхЃЌ
зїBBЁхЕФДЙжБЦНЗжЯпPFЃЌНЛOCгкPЃЌНЛABгкFЃЌДЫЪБBЁЂBЁхЙигкжБЯпPFЖдГЦЃЌТњзуЬѕМўЃЌ
дкRtЁїABBЁхжаЃЌЁпЁЯBABЁх=90ЁуЃЌBQ=QBЁхЃЌ
ЁрAQ=QBЃЌ
ЁрДЫЪБBЁЂAЃЈBЁфЃЉЙигкжБЯпMNЖдГЦЃЌТњзуЬѕМўЃЎ
ЁпCЃЈ2ЃЌ6ЃЉЃЌ
ЁржБЯпOCНтЮіЪНЮЊy=3xЃЌ
ЁпNMЁЮOAЃЌBN=NAЃЌ
ЁрCM=OMЃЌ
ЁрЕуMЃЈ1ЃЌ3ЃЉЃЌ
ЁрMN=5ЃЈЙ§MзіMM'ЁЭBAгкM'ЃЌРћгУЁїBB'AжаAB'=2ЁЬ3ЃЌAB=6ЃЌЫљвдЁЯB'BA=30ЁуЃЌНјЖјЭЦЕМЁЯM'MN=30ЁуЃЌЧѓЕУMNНсЙћИќПьЃЁЃЉ
ЁпBЃЈ6ЃЌ6ЃЉЃЌBЁхЃЈ2ЃЌ0ЃЉЃЌ
ЁрПЩЕУжБЯпBBЁхЕФНтЮіЪНЮЊy= ![]() xЉ3ЃЌ
xЉ3ЃЌ
ЁрЙ§ЕуQДЙжБBBЁхЕФжБЯпPFЕФНтЮіЪНЮЊy=Љ ![]() x+
x+ ![]() ЃЌ
ЃЌ
гЩ 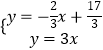 НтЕУ
НтЕУ 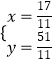 ЃЌ
ЃЌ
ЁрЕуPЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌFЃЈ6ЃЌ
ЃЉЃЌFЃЈ6ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрPF= ![]() =
= ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌелКлЕФГЄЮЊ5Лђ ![]()
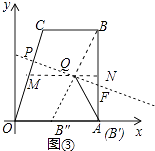
ЁОНтЮіЁПНтЃКЃЈ1ЃЉШчЭМ1жаЃЌBЕФЖдГЦЕуBЁфЃЌелКлЮЊMNЃЌMNНЛBBЁфгкHЃЎ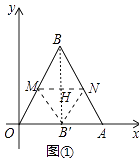
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌOBЁф=BЁфAЃЌ
ЁрBBЁфЁЭOAЃЌгжЁпBBЁфЁЭMNЃЌ
ЁрMNЁЮOAЃЌЁпBH=HBЁфЃЌ
ЁрBM=OMЃЌBN=NAЃЌ
ЁрMNЪЧЁїABCЕФжаЮЛЯпЃЌ
ЁрMN= ![]() OA=2ЃЎ
OA=2ЃЎ
ЙЪД№АИЮЊ2ЃЎ
ЃЈ1ЃЉШчЭМ1жаЃЌBЕФЖдГЦЕуBЁфЃЌелКлЮЊMNЃЌMNНЛBBЁфгкHЃЎжЛвЊжЄУїелКлЪЧЁїABCЕФжаЮЛЯпМДПЩЃЎЃЈ2ЃЉШчЭМ2жаЃЌBЕФЖдГЦЕуBЁфЃЌелКлЮЊMNЃЌMNНЛBBЁфгкHЃЌЧѓГіжБЯпMNЕФНтЮіЪНМДПЩНтОіЮЪЬтЃЎЃЈ3ЃЉДцдкЃЎШчЭМ3жаЃЌбгГЄBQНЛOAгкBЁхЃЌСЌНгAQЃЌЙ§ЕуQзїMNЁЮOAЃЌНЛOCгкMЃЌНЛABгкNЃЎПЩвджЄУїЯпЖЮMNМЦЫуелКлЃЛзїBBЁхЕФДЙжБЦНЗжЯпPFЃЌНЛOCгкPЃЌНЛABгкFЃЌДЫЪБBЁЂBЁхЙигкжБЯпPFЖдГЦЃЌЯпЖЮPFвВЪЧелКлЃЎЗжБ№ЧѓГіMNЁЂPFМДПЩНтОіЮЪЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫЗсИЛЩйФъЖљЭЏЕФвЕгрЩњЛюЃЌФГЩчЧјвЊдкШчЭМЫљЪОABЫљдкЕФжБЯпНЈвЛЭМЪщЪвЃЌБОЩчЧјгаСНЫљбЇаЃЫљдкЕФЮЛжУдкЕуCКЭЕуDДІЃЌCAЁЭABгкAЃЌDBЁЭABгкBЃЌвбжЊABЃН25kmЃЌCAЃН15kmЃЌDBЃН10kmЃЌЪдЮЪЃКЭМЪщЪвEгІИУНЈдкОрЕуAЖрЩйkmДІЃЌВХФмЪЙЫќЕНСНЫљбЇаЃЕФОрРыЯрЕШ?

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
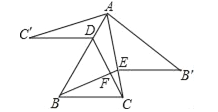
ЁОЬтФПЁПШчЭМЃЌШёНЧЁїABCжаЃЌDЃЌEЗжБ№ЪЧABЃЌACБпЩЯЕФЕуЃЌЁїADCЁеЁїADC'ЃЌЁїAEBЁеЁїAEB'ЃЌЧвC'DЁЮEB'ЁЮBCЃЌМЧBEЃЌCDНЛгкЕуFЃЌШєЁЯBACЃНxЁуЃЌдђЁЯBFCЕФДѓаЁЪЧ_____ЁуЃЎЃЈгУКЌxЕФЪНзгБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
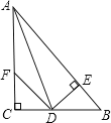
ЁОЬтФПЁПШчЭМЃКдкЁїABCжаЃЌЁЯC=90Ёу,ADЪЧЁЯBACЕФЦНЗжЯпЃЌDEЁЭABгкEЃЌFдкACЩЯЃЌBD=DFЃЛ
жЄУїЃКЃЈ1ЃЉCF=EBЃЎ
ЃЈ2ЃЉAB=AF+2EBЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїВЮМгФГЭјЕъЕФЁАЗХЦГщНБЁБЛюЖЏЃЌШчЭМЃЌЙВга4еХХЦЃЌЗжБ№ЖдгІ5дЊЃЌ10дЊЃЌ15дЊЃЌ20дЊЕФЯжН№гХЛнШЏЃЌаЁУїжЛФмПДЕНХЦЕФБГУцЃЎ 
ЃЈ1ЃЉШчЙћЫцЛњЗвЛеХХЦЃЌФЧУДГщжа20дЊЯжН№гХЛнШЏЕФИХТЪЪЧ ЃЎ
ЃЈ2ЃЉШчЙћЫцЛњЗСНеХХЦЃЌЧвЕквЛДЮЗЕФХЦВЛВЮгыЯТДЮЗХЦЃЌдђЫљЛёЯжН№гХЛнШЏЕФзмжЕВЛЕЭгк30дЊЕФИХТЪЪЧЖрЩйЃПЧыЛЪїзДЭМЛђСаБэИёЫЕУїЮЪЬтЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
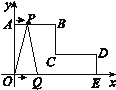
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌABЁЮCDЁЮxжсЃЌBCЁЮDEЁЮyжсЃЌЧвABЃНCDЃН4 cmЃЌOAЃН5 cmЃЌDEЃН2 cmЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы1 cmЕФЫйЖШЃЌбиABCТЗЯпЯђЕуCдЫЖЏЃЛЖЏЕуQДгЕуOГіЗЂЃЌвдУПУы2 cmЕФЫйЖШЃЌбиOEDТЗЯпЯђЕуDдЫЖЏЃЎШєPЃЌQСНЕуЭЌЪБГіЗЂЃЌЦфжавЛЕуЕНДяжеЕуЪБЃЌдЫЖЏЭЃжЙЃЎ
(1)жБНгаДГіBЃЌCЃЌDШ§ИіЕуЕФзјБъЃЛ
(2)ЕБPЃЌQСНЕуГіЗЂ3 sЪБЃЌЧѓШ§НЧаЮPQCЕФУцЛ§ЃЛ
(3)ЩшСНЕудЫЖЏЕФЪБМфЮЊt sЃЌгУКЌtЕФЪНзгБэЪОдЫЖЏЙ§ГЬжаШ§НЧаЮOPQЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉЃЈЉ2x3yЃЉ2ЃЈЉ2xyЃЉ+ЃЈЉ2x3yЃЉ3ЁТ2x2
ЃЈ2ЃЉ20202Љ2019ЁС2021
ЃЈ3ЃЉЃЈЉ2a+b+1ЃЉЃЈ2a+bЉ1ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЯТСаЪ§СПЙиЯЕСаВЛЕШЪНЃК
ЃЈ1ЃЉaгы1ЕФКЭЪЧе§Ъ§ ЃЛ
ЃЈ2ЃЉaЕФ![]() КЭbЕФ
КЭbЕФ![]() ЕФВюЪЧИКЪ§ ЃЛ
ЕФВюЪЧИКЪ§ ЃЛ
ЃЈ3ЃЉaгыbЕФСНЪ§КЭЕФЦНЗНВЛДѓгк9 ЃЛ
ЃЈ4ЃЉaЕФ![]() БЖгыbЕФКЭЕФЦНЗНЪЧЗЧИКЪ§ ЃЎ
БЖгыbЕФКЭЕФЦНЗНЪЧЗЧИКЪ§ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁСсКЭЕмЕмаЁЖЋЗжБ№ДгМвКЭЭМЪщЙнЭЌЪБГіЗЂЃЌбиЭЌвЛЬѕТЗЯрЯђЖјааЃЌаЁСсХмВНжаЭОИФЮЊВНааЃЌЕНДяЭМЪщЙнЧЁКУгУ30 min.аЁЖЋЦяздааГЕвд300 m/minЕФЫйЖШжБНгЛиМвЃЎСНШЫРыМвЕФТЗГЬy(m)гыИїздРыПЊГіЗЂЕиЕФЪБМфx(min)жЎМфЕФКЏЪ§ЭМЯѓШчЭМ9ЫљЪОЃЎ
ЃЈ1ЃЉМвгыЭМЪщЙнжЎМфЕФТЗГЬЮЊ mЃЌаЁСсВНааЕФЫйЖШЮЊ m/minЃЛ
ЃЈ2ЃЉЧѓаЁЖЋРыМвЕФТЗГЬyЙигкxЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЧѓСНШЫЯргіЕФЪБМфЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com