【题目】为了丰富少年儿童的业余生活，某社区要在如图所示AB所在的直线建一图书室，本社区有两所学校所在的位置在点C和点D处，CA⊥AB于A，DB⊥AB于B，已知AB＝25km，CA＝15km，DB＝10km，试问：图书室E应该建在距点A多少km处，才能使它到两所学校的距离相等?
科目：初中数学 来源： 题型：
【题目】【知识背景】在学习计算框图时，可以用“ 
”表示数据输入、输出框；用“ 
”表示数据处理和运算框；用“ 
”表示数据判断框（根据条件决定执行两条路径中的某一条） 
（1）【尝试解决】 ①如图1，当输入数x=﹣2时，输出数y=
②如图2，第一个“ ”内，应填； 第二个“ ”内，应填；
（2）①如图3，当输入数x=﹣1时，输出数y=； ②如图4，当输出的值y=17，则输入的值x=
（3）【实际应用】 为鼓励节约用水，决定对用水实行“阶梯价”：当每月用水量不超过10吨时（含10吨），以3元/吨的价格收费；当每月用水量超过10吨时，超过部分以4元/吨的价格收费．请设计出一个“计算框图”，使得输入数为用水量x，输出数为水费y．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）数学爱好者小森偶然阅读到这样一道竞赛题：
一个圆内接六边形ABCDEF，各边长度依次为 3，3，3，5，5，5，求六边形ABCDEF的面积．
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理，将六边形进行分割重组，得到图③．可以求出六边形ABCDEF的面积等于 ．
（2）类比探究：一个圆内接八边形，各边长度依次为2，2，2，2，3，3，3，3．求这个八边形的面积．请你仿照小森的思考方式，求出这个八边形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图,有一块塑料矩形模板ABCD，长为10cm，宽为4cm，将你手中足够大的直角三角板 PHF 的直角顶点P落在AD边上(不与A、D重合)，在AD上适当移动三角板顶点P:
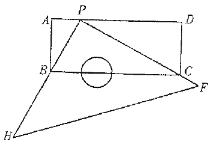
①能否使你的三角板两直角边分别通过点B与点C?若能，请你求出这时 AP 的长；若不能，请说明理由；
②再次移动三角板位置，使三角板顶点P在AD上移动，直角边PH 始终通过点B，另一直角边PF与DC的延长线交于点Q，与BC交于点E，能否使CE=2cm?若能，请你求出这时AP的长；若不能，请你说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图1是一个长为2x、宽为2y的长方形，沿图中虚线用剪刀剪成四个完全相同的小长方形，然后按图2所示拼成一个正方形．
（1）你认为图2中的阴影部分的正方形的边长等于
（2）试用两种不同的方法求图2中阴影部分的面积．
方法1： 方法2：
（3）根据图2你能写出下列三个代数式之间的等量关系吗？
代数式：（x+y）2，（x-y）2，4xy．
（4）根据（3）题中的等量关系，解决如下问题：
若x+y=4，xy=3，则（x-y）2=
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点A，B，C在平面直角坐标系中的坐标分别为(5，5)，(3，2)，(6，3)．
(1)作△ABC关于直线l：x＝1对称的△A1B1C1，点A，B，C的对称点分别是A1，B1，C1；
(2)点A1的坐标为__________，
点B1的坐标为__________，
点C1的坐标为__________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知点A（m，n）在y=
的图象上，且m（n﹣1）≥0．
（1）求m的取值范围；
（2）当m，n为正整数时，写出所有满足题意的A点坐标，并从中随机抽取一个点，求：在直线y=﹣x+6下方的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
