
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�AB��CD��x�ᣬBC��DE��y�ᣬ��AB��CD��4 cm��OA��5 cm��DE��2 cm������P�ӵ�A��������ÿ��1 cm���ٶȣ���ABC·�����C�˶�������Q�ӵ�O��������ÿ��2 cm���ٶȣ���OED·�����D�˶�����P��Q����ͬʱ����������һ�㵽���յ�ʱ���˶�ֹͣ��
(1)ֱ��д��B��C��D����������ꣻ
(2)��P��Q�������3 sʱ����������PQC�������
(3)�������˶���ʱ��Ϊt s���ú�t��ʽ�ӱ�ʾ�˶�������������OPQ�������
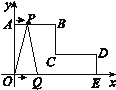
���𰸡���1��B��4��5����C��4��2����D��8��2������2��2����3�� ![]() .
.
��������
��1������ƽ��ֱ������ϵд����������꼴�ɣ�
��2���������P��Q�����꣬�����CP��CQ��Ȼ����������ε������ʽ��ʽ���㼴�ɵý⣻
��3���������P��A�˶���C��ʱ��Ҫ7�룬��Q��O�˶���D��ʱ��Ҫ5�룬��������һ�㵽���յ�ʱ���˶�ֹͣ����֪�˶�ʱ��t��ȡֵ��ΧΪ0��t��5��Ȼ�������������ۼ���.��������ֱ�Ϊ��0��t��4����ʱ��P��AB�ϣ���Q��OE�ϣ���4��t��5����ʱ��P��BC�ϣ���Q��DE��.
(1)��AB��CD��x�ᣬBC��DE��y�ᣬ��AB=CD=4��OA=5��DE=2��
4+4=8��
��B(4��5)��C(4��2)��D(8��2)��
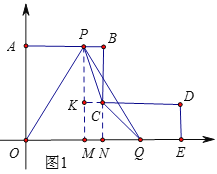
(2)��P��Q�����˶�3 sʱ����ͼ1����ʱ��P(3��5)��Q(6��0)��
��ΪC(4��2)������P��PM��x�ᣬ�ӳ�BC��x���ڵ�N���ӳ�DC��PM�ڵ�K��
����M(3��0)��N��4��0����K��3��2����
����QM��MQ=3��CK=MN=1��PK=BC=3��CN=NQ=2��
����������PQC�������![]() ��3��5��
��3��5��![]() ��1��3��
��1��3��![]() ��2��2��2��1��2��
��2��2��2��1��2��
(3)��P�˶���·����ΪAB+BC=4+3=7����ʱ��Ҫ7�룬
��Q�˶���·����ΪOE+DE=8+2=10����ʱ��Ҫ5�룬
��������һ�㵽���յ�ʱ���˶�ֹͣ����֪�˶�ʱ��t��ȡֵ��ΧΪ0��t��5��
�ٵ�0��t��4ʱ(��ͼ2)��OA��5��OQ��2t��
S������OPQ��![]() OQOA��
OQOA��![]() ��2t��5��5t������
��2t��5��5t������
�ڵ�4��t��5ʱ(��ͼ3)��OE��8��EM��9��t��PM��4��MQ��17��3t��EQ��2t��8��
S������OPQ��S����OPME��S������PMQ��S������OEQ
��![]() ��(4��8)��(9��t)��
��(4��8)��(9��t)��![]() ��4��(17��3t)��
��4��(17��3t)��![]() ��8��(2t��8)
��8��(2t��8)
��52��8t��
���ϣ�![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��2��0����B��0��4��������BOC��ʹ��BOC����ABOȫ�ȣ����C����Ϊ_____________������C�����A�غϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
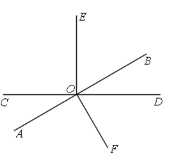
����Ŀ����֪��ͼ��ֱ��AB��CD�ཻ�ڵ�O����COE=90�㣬����BOD:��BOC=1:5��
��1�����AOC�Ķ�����
��2����ͼ������O��OF��AB,���DOF���EOF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(��������10��)�Ķ����в��ϣ�
��1������x�ķ���x2-3x+1=0��x��0����������ͬʱ����![]() �ã�
�ã� ![]() ��
��![]() ��
�� ![]() ��
��
��2��a3+b3=��a+b����a2-ab+b2����a3-b3=��a-b����a2+ab+b2����
�������ϲ��ϣ�����������⣺
��1��x2-4x+1=0��x��0������![]() = ______ ��
= ______ �� ![]() = ______ ��
= ______ �� ![]() = ______ ��
= ______ ��
��2��2x2-7x+2=0��x��0������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽����
��1����ͼ�٣��߳�Ϊ4�ĵȱߡ�OABλ��ƽ��ֱ������ϵ�У�����OAB�۵���ʹ��B����OA���е㴦�����ۺ۳�Ϊ��
��2����ͼ�ڣ�����OABCλ��ƽ��ֱ������ϵ�У�����OA=8��AB=6�����������߶�MN�۵�����B����x���ϣ�����AN= ![]() AB�����ۺ�MN�ij���
AB�����ۺ�MN�ij���
��3����ͼ�ۣ��ı���OABCλ��ƽ��ֱ������ϵ�У�����OA=AB=6��CB=4��BC��OA��AB��OA�ڵ�A����Q��4��3��Ϊ�ı����ڲ�һ�㣬���ı����۵���ʹ��B����x���ϣ����Ƿ���ڹ���Q���ۺۣ������ڣ�����ۺ۳����������ڣ���˵�����ɣ�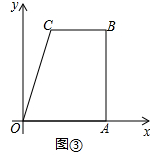
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ܡ���ѻ��ˮ�����µ�������������Ͳ�������ͬ��С����������²�����

�����ͼ�и�������Ϣ������������⣺
(1)����һ��С������Ͳ��ˮ������_____________________________ cm��
(2)��Ͳ�����ٷ��뼸��С��ʱ��ˮ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC����ABD�Ľ�ƽ���ߣ�BC=DC����A=��E=30�㣬��D=50�㣮
��1��д��AB=DE�����ɣ�
��2������BCE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=ax+b��˫����y= ![]() ��x��0������A��x1 �� y1����B��x2 �� y2�����㣨A��B���غϣ���ֱ��AB��x�ύ��P��x0 �� 0������y�ύ�ڵ�C��
��x��0������A��x1 �� y1����B��x2 �� y2�����㣨A��B���غϣ���ֱ��AB��x�ύ��P��x0 �� 0������y�ύ�ڵ�C�� 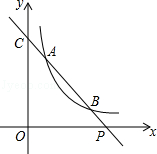
��1����A��B��������ֱ�Ϊ��1��3������3��y2�������P�����꣮
��2����b=y1+1����P������Ϊ��6��0������AB=BP����A��B��������꣮
��3����ϣ�1������2���еĽ�������벢�õ�ʽ��ʾx1 �� x2 �� x0֮��Ĺ�ϵ����Ҫ��֤������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD��ƽ���ı��Σ������н����в���ȷ����(����)
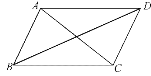
A. ��AB��BCʱ���ı���ABCD������
B. ��AC��BDʱ���ı���ABCD������
C. ����ABC��90��ʱ���ı���ABCD�Ǿ���
D. ��AC��BDʱ���ı���ABCD��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com