
【题目】小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:

请根据图中给出的信息,解答下列问题:
(1)放入一个小球,量筒中水面升高_____________________________ cm;
(2)量筒中至少放入几个小球时有水溢出?
【答案】(1)2 (2)10个
【解析】
(1)比较第一、二两个量筒可知,放入三个球,水面上升6cm,由此可求放入一个小球量筒中水面升高的高度;
(2)设量筒中水面的高度y(cm)与小球个数x的函数关系为y=kx+b,根据量筒中水面的高度y(cm)=量筒原来的高度+放入的小球增长的高度,就可以求出解析式;得出y>49,再进行求解即可得出答案.
根据题意得:
(36-30)÷3=2(cm).
答:放入一个小球量筒中水面升高2cm;
(2)设量筒中水面的高度y(cm)与小球个数x的函数关系为y=kx+b,由题意,得
![]() ,
,
解得:![]() .
.
则放入小球后量筒中水面的高度y(cm)与小球个数x(个)之间的一次函数关系式是:y=30+2x;由题意,得
30+2x>49,
解得:x>9.5,
∵x为整数,
∴x最小为10.
答:量筒中至少放入10个小球时有水溢出.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选取最关注的一个),根据调查结果绘制了两幅不完整的统计图,根据图中提供的信息,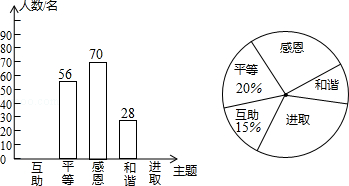
解答下列问题:
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整;并写出这次主题班会调查结果的众数是;中位数落在的区域是 .
(3)若该校学生人数为800人,请根据上述调查结果,估计该校学生中“感恩”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).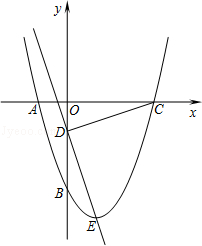
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
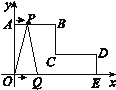
【题目】如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4 cm,OA=5 cm,DE=2 cm,动点P从点A出发,以每秒1 cm的速度,沿ABC路线向点C运动;动点Q从点O出发,以每秒2 cm的速度,沿OED路线向点D运动.若P,Q两点同时出发,其中一点到达终点时,运动停止.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发3 s时,求三角形PQC的面积;
(3)设两点运动的时间为t s,用含t的式子表示运动过程中三角形OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在运动会前夕,育红中学都会购买篮球、足球作为奖品.若购买10个篮球和15个足球共花费3000元,且购买一个篮球比购买一个足球多花50元.
(1)求购买一个篮球,一个足球各需多少元?
(2)今年学校计划购买这种篮球和足球共10个,恰逢商场在搞促销活动,篮球打九折,足球打八五折,若此次购买两种球的总费用不超过1050元,则最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
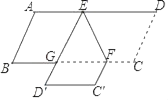
【题目】如图,E,F分别是ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折得到EFC′D′,ED′交BC于点C,则△GEF的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
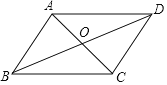
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点E处,那么S△AED=______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共300人参加一次大型公益活动,如果租用6辆大客车和5辆小客车,恰好全部坐满,已知每辆大客车的乘客座位数比小客车多17个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了30人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,且所有参加活动的师生都有座位,求租用小客车数量的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com