
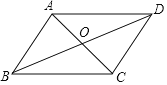
【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,∠AOB=60°,BD=4,将△ABC沿直线AC翻折后,点B落在点E处,那么S△AED=______
【答案】![]()
【解析】
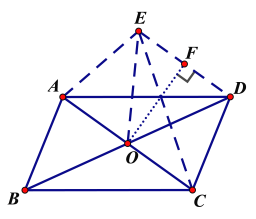
根据题意画出翻折后的图形,连接OE、DE,先证明△OED是等边三角形,再利用同底等高的三角形面积相等,说明S△AED=S△OED,作OF⊥ED于F,求出△OED的面积即可得出结果.
解:如图,△AEC是△ABC沿AC翻折后的图形,连接OE、DE,
∵四边形ABCD是平行四边形,
∴OB=OD=![]() BD=2,
BD=2,
∵△AEC是△ABC沿AC翻折后的图形,∠AOB=60,
∴∠AOE=60,OE=OB,
∴∠EOD=60,OE=OD,
∴△OED是等边三角形,
∴∠DEO=∠AOE=60,ED=OD=2,
∴ED∥AC,
∴S△AED=S△OED,
作OF⊥ED于F,DF=![]() ED=1,
ED=1,
∴OF=![]() =
=![]() ,
,
∴S△OED=![]() ED·DF=
ED·DF=![]()
∴S△AED=![]() .
.
故答案为:![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知∠BOP与OP上点C,点A(在点C的右边),李玲现进行如下操作:①以点O为圆心,OC长为半径画弧,交OB于点D;②以点A为圆心,OC长为半径画弧MN,交OA于点M;③以点M为圆心,CD长为半径画弧,交弧MN于点E,作射线AE,操作结果如图所示,下列结论不能由上述操作结果得出的是( ).
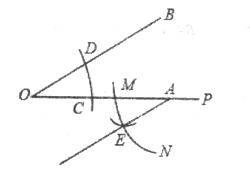
A. ∠ACD=∠EAP B. ∠ODC=∠AEM C. OB∥AE D. CD∥ME
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明受《乌鸦喝水》故事的启发,利用量筒和体积相同的小球进行了如下操作:

请根据图中给出的信息,解答下列问题:
(1)放入一个小球,量筒中水面升高_____________________________ cm;
(2)量筒中至少放入几个小球时有水溢出?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“小组合作学习”成为我区推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“小组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下: 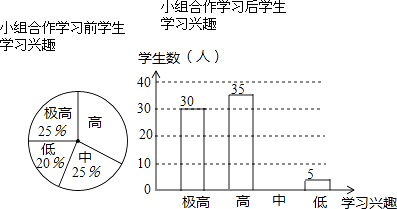
请结合图中信息解答下列问题:
(1)小组合作学习前学生学习兴趣为“高”的所占的百分比为;
(2)补全小组合作学习后学生学习兴趣的统计图;
(3)通过“小组合作学习”前后学生学习兴趣的对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=ax+b与双曲线y= ![]() (x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C. 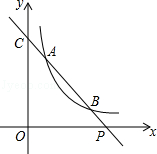
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1 , x2 , x0之间的关系(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=2x+4的图象与x,y轴分别相交于点A,B,以AB为边作正方形ABCD(点D落在第四象限).
(1)求点A,B,D的坐标;
(2)联结OC,设正方形的边CD与x相交于点E,点M在x轴上,如果△ADE与△COM全等,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年怀柔区中考体育加试女子800米耐力测试中,同时起跑的李丽和吴梅所跑的路程![]() 米
米![]() 与所用时间
与所用时间![]() 秒
秒![]() 之间的函数图象分别为线段OA和折线
之间的函数图象分别为线段OA和折线![]() 下列说法正确的是
下列说法正确的是![]()
![]()
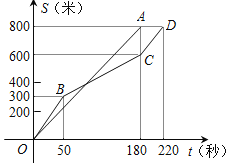
A. 李丽的速度随时间的增大而增大
B. 吴梅的平均速度比李丽的平均速度大
C. 在起跑后180秒时,两人相遇
D. 在起跑后50秒时,吴梅在李丽的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ABCD是菱形,△EFP的顶点E,F,P分别在线段AB,AD,AC上,且EP=FP. 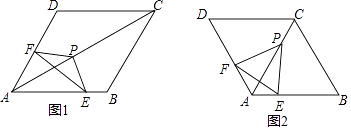
(1)证明:∠EPF+∠BAD=180°;
(2)若∠BAD=120°,证明:AE+AF=AP;
(3)若∠BAD=θ,AP=a,求AE+AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的符号表示下面的关系:
(1)a的一半比a与3的差小. (2)x的![]() 与5的差小于1.
与5的差小于1.
(3)x与6的和大于-7. (4)8与y的2倍的和是正数.
(5)a的3倍与7的差是负数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com