
【题目】如图,已知BC是△ABD的角平分线,BC=DC,∠A=∠E=30°,∠D=50°.
(1)写出AB=DE的理由;
(2)求∠BCE的度数.

【答案】(1)证明见解析(2)20°
【解析】
由三角形内角和定理可得∠DBA=100°,由BC是∠DBA的角平分线可得∠ABC=50°,即可证明∠ABC=∠D,通过AAS可证明△ABC≌△EDC,即可得AB=DE;(2)由∠DBC=50°,∠E=30°,根据三角形外角性质即可求出∠BCE的度数.
(1)∵∠A=30°,∠D=50°,
∴∠DBA=180°-30°-50°=100°,
∵BC是∠DBA的角平分线,
∴∠DBC=∠ABC=50°,
∴∠ABC=∠D,
∵BC=CD,∠A=∠E,∠ABC=∠D,
∴△ABC≌△EDC(AAS),
∴AB=DE.
(2)∵∠DBC=50°,∠E=30°,
∴∠BCE=∠DBC-∠E=50°-30°=20°.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
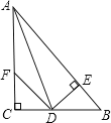
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
证明:(1)CF=EB.
(2)AB=AF+2EB.
查看答案和解析>>
科目:初中数学 来源: 题型:
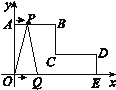
【题目】如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4 cm,OA=5 cm,DE=2 cm,动点P从点A出发,以每秒1 cm的速度,沿ABC路线向点C运动;动点Q从点O出发,以每秒2 cm的速度,沿OED路线向点D运动.若P,Q两点同时出发,其中一点到达终点时,运动停止.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发3 s时,求三角形PQC的面积;
(3)设两点运动的时间为t s,用含t的式子表示运动过程中三角形OPQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣2x3y)2(﹣2xy)+(﹣2x3y)3÷2x2
(2)20202﹣2019×2021
(3)(﹣2a+b+1)(2a+b﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
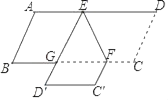
【题目】如图,E,F分别是ABCD的边AD,BC上的点,EF=6,∠DEF=60°,将四边形EFCD沿EF翻折得到EFC′D′,ED′交BC于点C,则△GEF的周长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列数量关系列不等式:
(1)a与1的和是正数 ;
(2)a的![]() 和b的
和b的![]() 的差是负数 ;
的差是负数 ;
(3)a与b的两数和的平方不大于9 ;
(4)a的![]() 倍与b的和的平方是非负数 .
倍与b的和的平方是非负数 .
查看答案和解析>>
科目:初中数学 来源: 题型:
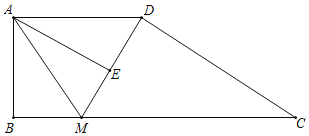
【题目】已知,梯形ABCD中,AD∥BC,∠ABC=90°,AB=3,BC=10,AD=5,M是BC边上的任意一点,联结DM,联结AM.
(1)若AM平分∠BMD,求BM的长;
(2)过点A作AE⊥DM,交DM所在直线于点E.
①设BM=x,AE=y求y关于x的函数关系式;
②联结BE,当△ABE是以AE为腰的等腰三角形时,请直接写出BM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com