
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为_____________.(点C不与点A重合)
科目:初中数学 来源: 题型:
【题目】如图,已知A(2,3),B(1,1),C(4,1),M(6,3).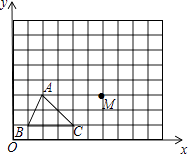
(1)将△ABC平原得到△A1B1C1 , 其中点A,B,C的对应点分别是A1 , B1 , C1 , 且点A1的坐标是(3,6),在图中画出△A1B1C1 .
(2)将(1)中的△A1B1C1绕点M顺时针旋转90°,画出旋转后的△A2B2C2(其中点A2 , B2 , C2的对应点分别是A1 , B1 , C1),并写出点A2 , B2 , C2的坐标.
(3)(2)中的△A2B2C2能通过旋转△ABC得到吗?若能,请写出旋转的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x= ![]() ,且经过点(2,0),下列说法: ①abc<0;
,且经过点(2,0),下列说法: ①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(﹣2,y1),(﹣3,y2)是抛物线上的两点,则y1<y2 ,
其中说法正确的是( )
A.①②④
B.③④
C.①③④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC 中,AB=AC,∠BAC=90°,D 是BC 上一点,EC⊥BC,EC=BD,DF=FE.
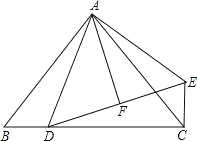
求证:(1)△ABD≌△ACE;
(2)AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,铅球运行路线如图.
,铅球运行路线如图. 
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.已知,如图:在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O ![]() C
C ![]() B
B ![]() A运动,点P的运动时间为t秒.
A运动,点P的运动时间为t秒.

(1)当t=2时,求直线PD的解析式。
(2)当P在BC上,OP+PD有最小值时,求点P的坐标。
(3)当t为何值时,△ODP是腰长为5的等腰三角形?(直接写出t的值).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖南路大桥于今年5月1日竣工,为徒骇河景区增添了一道亮丽的风景线 . 某校数学兴趣小组用测量仪器测量该大桥的桥塔高度,在距桥塔AB底部50米的C处,测得桥塔顶部A的仰角为41.5°(如图) . 已知测量仪器CD的高度为1米,则桥塔AB的高度约为( )(参考数据:sin41.5°≈0.663,cos41.5°≈0.749,tan41.5°≈0.885)
A.34米
B.38米
C.45米
D.50米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com