
【题目】解方程:x2﹣4x+3=0.
【答案】解法一:移项得 x2﹣4x=﹣3,
配方得 x2﹣4x+4=﹣3+4,
∴(x﹣2)2=1,
即 x﹣2=1或x﹣2=﹣1,
∴x1=3,x2=1;
解法二:∵a=1,b=﹣4,c=3,
∴b2﹣4ac=(﹣4)2﹣4×1×3=4>0,
∴ ![]() ,
,
∴x1=3,x2=1;
解法三:原方程可化为 (x﹣1)(x﹣3)=0,
∴x﹣1=0或x﹣3=0,
∴x1=1,x2=3.
【解析】此题可以采用配方法:首先将常数项3移到方程的左边,然后再在方程两边同时加上4,即可达到配方的目的,继而求得答案;
此题也可采用公式法:注意求根公式为把x= ![]() ,解题时首先要找准a,b,c;
,解题时首先要找准a,b,c;
此题可以采用因式分解法,利用十字相乘法分解因式即可达到降幂的目的.
【考点精析】关于本题考查的配方法和公式法,需要了解左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;要用公式解方程,首先化成一般式.调整系数随其后,使其成为最简比.确定参数abc,计算方程判别式.判别式值与零比,有无实根便得知.有实根可套公式,没有实根要告之才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】李大爷一年前买入了A、B两种兔子共46只.目前,他所养的这两种兔子数量相同,且A种兔子的数量比买入时减少了3只,B种兔子的数量比买入时减少a只.
(1)则一年前李大爷买入A种兔子________只,目前A、B两种兔子共________只(用含a的代数式表示);
(2)若一年前买入的A种兔子数量多于B种兔子数量,则目前A、B两种兔子共有多少只?
(3)李大爷目前准备卖出30只兔子,已知卖A种兔子可获利15元/只,卖B种兔子可获利6元/只.如果卖出的A种兔子少于15只,且总共获利不低于280元,那么他有哪几种卖兔方案?哪种方案获利最大?请求出最大获利.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠2=180°( ), +∠EFD=180°(邻补角定义),
∴ (同角的补角相等)
∴AB∥ (内错角相等,两直线平行)
∴∠ADE=∠3( )
∵∠3=∠B(已知)∴ (等量代换)
∴ ∥BC(同位角相等,两直线平行)
∴∠AED=∠C( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有客房200间供游客居住,当每间客房的定价为每天180元时,客房恰好全部住满;如果每间客房每天的定价每增加10元,就会减少4间客房出租.设每间客房每天的定价增加x元,宾馆出租的客房为y间.求:
(1)y关于x的函数关系式;
(2)如果某天宾馆客房收入38400元,那么这天每间客房的价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
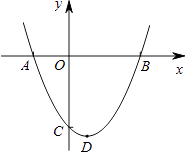
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴相交于点A(﹣2,0)和点B,与y轴相交于点C,顶点D(1,﹣ ![]() )
)
(1)求抛物线对应的函数关系式;
(2)求四边形ACDB的面积;
(3)若平移(1)中的抛物线,使平移后的抛物线与坐标轴仅有两个交点,请直接写出一个平移后的抛物线的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为_____________.(点C不与点A重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB , 垂足为D , AB=c , ∠a=α , 则CD长为( ) 
A.csin2α
B.ccos2α
C.csinαtanα
D.csinαcosα
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com