
【题目】如图,∠A=∠B=50°,P 为 AB 中点,点 M 为射线 AC 上(不与点 A 重合)的任意一点,连接 MP, 并使MP 的延长线交射线BD 于点N,设∠BPN=α.

(1)求证:△APM≌△BPN;
(2)当 MN=2BN 时,求α的度数;
(3)若△BPN 为锐角三角形时,直接写出α的取值范围.
【答案】(1)证明见解析;(2)α=∠B=50°;(3)40°<α<90°.
【解析】
根据AAS可证明△APM≌△BPN.
由(1)中的全等得MN=2PN,所以BN=PN,由等边对等角可得结论.
三角形的外心是外接圆的圆心,三边垂直平分线的交点,直角三角形的外心在直角顶点上,钝角三角形的外心在三角形内部,只有锐角三角形的外心在三角形的内部,所以根据题目中要求可知:△BPN是锐角三角形,由三角形的内角和可得结论.
(1)∵P是AB的中点,
∴PA=PB,
在△APM和△BPN中,
∵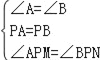 ,
,
∴△APM≌△BPN(ASA);
(2)由(1)得:△APM≌△BPN,
∴PM=PN,
∴MN=2PN,
∵MN=2BN,
∴BN=PN,
∴α=∠B=50°;
(3)∵△BPN是锐角三角形,
∵∠B=50°,
∴40°<∠BPN<90°,即40°<α<90°.


科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2)
(1)写出点A、B的坐标:A( , )、B( , )
(2)将△ABC先向左平移1个单位长度,再向上平移2个单位长度,得到△A′B′C′,画出△A′B′C′
(3)写出三个顶点坐标A′( 、 )、B′( 、 )、C′ ( 、 )
(4)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b经过点B(1,4),且与直线y=﹣x﹣11平行.
(1)求直线AB的解析式并求出点C的坐标;
(2)根据图象,写出关于x的不等式0<2x﹣4<kx+b的解集;
(3)现有一点P在直线AB上,过点P作PQ∥y轴交直线y=2x﹣4于点Q,若线段PQ的长为3,求P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,直线
,直线![]() ,
, ![]() 交于点
交于点![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求![]() 的面积;
的面积;
(4)在直线![]() 上存在异于点
上存在异于点![]() 的另一点
的另一点![]() ,使得
,使得![]() 与
与![]() 的面积相等,请直接写出点
的面积相等,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察推理:如图 1,△ABC 中,∠ACB=90°,AC=BC,直线 L 过点C,点 A,B 在直线 L 同侧,BD⊥L, AE⊥L,垂足分别为D,E
求证:△AEC≌△CDB
(2)类比探究:如图 2,Rt△ABC 中,∠ACB=90°,AC=4,将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C,求△AB’C 的面积
(3)拓展提升:如图 3,等边△EBC 中,EC=BC=3cm,点 O 在 BC 上且 OC=2cm,动点 P 从点 E 沿射线EC 以 1cm/s 速度运动,连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF,设点 P 运动的时间为t 秒。
当t= 秒时,OF∥ED

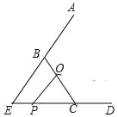
若要使点F 恰好落在射线EB 上,求点P 运动的时间t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名男生推铅球,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是y=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,铅球运行路线如图.
,铅球运行路线如图. 
(1)求铅球推出的水平距离;
(2)通过计算说明铅球行进高度能否达到4m?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,﹣3),(2,5),(﹣1,﹣4)且与x轴交于A、B两点,其顶点为P. 
(1)试确定此二次函数的解析式;
(2)根据函数的图象,指出函数的增减性,并直接写出函数值y<0时自变量x的取值范围.
(3)求△ABP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E , 再从E沿着垂直于AE的方向走到F , C为AE上一点,其中3位同学分别测得三组数据:①AC , ∠ACB;②EF.DE.AD;③CD , ∠ACB , ∠ADB.其中能根据所测数据求得A.B两树距离的有( )
A.0组
B.一组
C.二组
D.三组
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com