
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
∴y= ![]() (x+1)(x﹣3).
(x+1)(x﹣3).
∴A(﹣1,0),B(3,0).
当x=4时,y= ![]() .
.
∴E(4, ![]() ).
).
设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得: 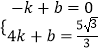 ,
,
解得:k= ![]() ,b=
,b= ![]() .
.
∴直线AE的解析式为y= ![]() x+
x+ ![]() .
.
(2)
解:设直线CE的解析式为y=mx﹣ ![]() ,将点E的坐标代入得:4m﹣
,将点E的坐标代入得:4m﹣ ![]() =
= ![]() ,解得:m=
,解得:m= ![]() .
.
∴直线CE的解析式为y= ![]() x﹣
x﹣ ![]() .
.
过点P作PF∥y轴,交CE与点F.
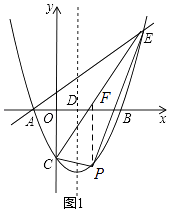
设点P的坐标为(x, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ),则点F(x,
),则点F(x, ![]() x﹣
x﹣ ![]() ),
),
则FP=( ![]() x﹣
x﹣ ![]() )﹣(
)﹣( ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() )=
)= ![]() x2+
x2+ ![]() x.
x.
∴△EPC的面积= ![]() ×(
×( ![]() x2+
x2+ ![]() x)×4=﹣
x)×4=﹣ ![]() x2+
x2+ ![]() x.
x.
∴当x=2时,△EPC的面积最大.
∴P(2,﹣ ![]() ).
).
如图2所示:作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.
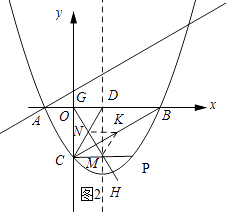
∵K是CB的中点,
∴k( ![]() ,﹣
,﹣ ![]() ).
).
∵点H与点K关于CP对称,
∴点H的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
∵点G与点K关于CD对称,
∴点G(0,0).
∴KM+MN+NK=MH+MN+GN.
当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.
∴GH= ![]() =3.
=3.
∴KM+MN+NK的最小值为3.
(3)
解:如图3所示:
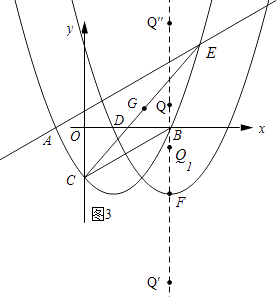
∵y′经过点D,y′的顶点为点F,
∴点F(3,﹣ ![]() ).
).
∵点G为CE的中点,
∴G(2, ![]() ).
).
∴FG= ![]() =
= ![]() .
.
∴当FG=FQ时,点Q(3, ![]() ),Q′(3,
),Q′(3, ![]() ).
).
当GF=GQ时,点F与点Q″关于y= ![]() 对称,
对称,
∴点Q″(3,2 ![]() ).
).
当QG=QF时,设点Q1的坐标为(3,a).
由两点间的距离公式可知:a+ ![]() =
= ![]() ,解得:a=﹣
,解得:a=﹣ ![]() .
.
∴点Q1的坐标为(3,﹣ ![]() ).
).
综上所述,点Q的坐标为(3, ![]() )或′(3,
)或′(3, ![]() )或(3,2
)或(3,2 ![]() )或(3,﹣
)或(3,﹣ ![]() ).
).
【解析】(1)抛物线的解析式可变形为y= ![]() (x+1)(x﹣3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入求得k和b的值,从而得到AE的解析式;(2)设直线CE的解析式为y=mx﹣
(x+1)(x﹣3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入求得k和b的值,从而得到AE的解析式;(2)设直线CE的解析式为y=mx﹣ ![]() ,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE与点F.设点P的坐标为(x,
,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE与点F.设点P的坐标为(x, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ),则点F(x,
),则点F(x, ![]() x﹣
x﹣ ![]() ),则FP=
),则FP= ![]() x2+
x2+ ![]() x.由三角形的面积公式得到△EPC的面积=﹣
x.由三角形的面积公式得到△EPC的面积=﹣ ![]() x2+
x2+ ![]() x,利用二次函数的性质可求得x的值,从而得到点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.然后利用轴对称的性质可得到点G和点H的坐标,当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH;(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为QG=FG、QG=QF,FQ=FQ三种情况求解即可.
x,利用二次函数的性质可求得x的值,从而得到点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.然后利用轴对称的性质可得到点G和点H的坐标,当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH;(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为QG=FG、QG=QF,FQ=FQ三种情况求解即可.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如表:
加数的个数n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=15=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)根据表中的规律猜想:用n的式子表示S的公式为:S=2+4+6+8+…+2n=;
(2)如下数表是由从1开始的连续自然数组成,观察规律:
①第n行的第一个数可用含n的式子表示为;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现:
(1)若直线a1⊥a2,a2∥a3,则直线a1与a3的位置关系是__________,请说明理由.
(2)若直线a1⊥a2,a2∥a3,a3⊥a4,则直线a1与a4的位置关系是________.(直接填结论,不需要证明)
(3)现在有2 011条直线a1,a2,a3,…,a2 011,且有a1⊥a2,a2∥a3,a3⊥a4,a4∥a5…,请你探索直线a1与a2 011的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC. 

(1)如图1,若AB=3 ![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
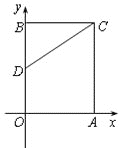
【题目】如图,在平面直角坐标系中,长方形![]() 的顶点
的顶点![]() 在坐标原点,顶点
在坐标原点,顶点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 是边
是边![]() 上的一个动点,当
上的一个动点,当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为_________.
的坐标为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间有一条笔直的公路![]() ,小明从甲地出发沿公路
,小明从甲地出发沿公路![]() 步行前往乙地,同时小亮从乙地出发沿公路
步行前往乙地,同时小亮从乙地出发沿公路![]() 骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为
骑车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为![]() (m),小亮与甲地的距离为
(m),小亮与甲地的距离为![]() (m),小明与小亮之间的距离为
(m),小明与小亮之间的距离为![]() (m),小明行走的时间为
(m),小明行走的时间为![]() (min).
(min).![]() ,
,![]() 与
与![]() 之间的函数图象如图①,
之间的函数图象如图①,![]() 与
与![]() 之间的函数图象(部分)如图②.
之间的函数图象(部分)如图②.
(1)求小亮从乙地到甲地过程中![]() (m)与
(m)与![]() (min)之间的函数表达式;
(min)之间的函数表达式;
(2)求小亮从甲地返回到与小明相遇的过程中![]() (m)与
(m)与![]() ( min)之间的函数表达式;
( min)之间的函数表达式;
(3)在图②中,补全整个过程中![]() (m)与
(m)与![]() (min)之间的函数图象,并确定
(min)之间的函数图象,并确定![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况. 他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
分组 | 频数 | 百分比 |
600≤ | 2 | 5% |
800≤ | 6 | 15% |
1000≤ | 45% | |
9 | 22.5% | |
1600≤ | 2 | |
合计 | 40 | 100% |

根据以上提供的信息,解答下列问题:
(1)补全频数分布表.
(2)补全频数分布直方图.
(3)绘制相应的频数分布折线图.
(4)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.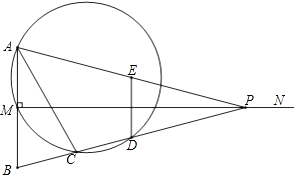
(1)当∠APB=28°时,求∠B和 ![]() 的度数;
的度数;
(2)求证:AC=AB.
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com