
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC. 

(1)如图1,若AB=3 ![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
【答案】
(1)∵∠ABM=45°,AM⊥BM,
∴AM=BM=ABcos45°=3 ![]() ×
× ![]() =3,
=3,
则CM=BC﹣BM=5﹣2=2,
∴AC= ![]() =
= ![]() =
= ![]() ;
;
(2)延长EF到点G,使得FG=EF,连接BG.
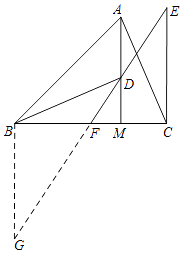
由DM=MC,∠BMD=∠AMC,BM=AM,
∴△BMD≌△AMC(SAS),
∴AC=BD,
又CE=AC,
因此BD=CE,
由BF=FC,∠BFG=∠EFC,FG=FE,
∴△BFG≌△CFE,
故BG=CE,∠G=∠E,
所以BD=BG=CE,
因此∠BDG=∠G=∠E.
【解析】(1)先由AM=BM=ABcos45°=3可得CM=2,再由勾股定理可得AC的长;(2)延长EF到点G,使得FG=EF,证△BMD≌△AMC得AC=BD,再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠E.
【考点精析】关于本题考查的勾股定理的概念,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )
A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.截长就是在长边上截取一条线段与某一短边相等,补短就是通过延长或旋转等方式使两条短边拼合到一起,从而解决问题.
(1)如图1,△ABC是等边三角形,点D是边BC下方一点,∠BDC=120°,探索线段DA、DB、DC之间的数量关系.
解题思路:延长DC到点E,使CE=BD,根据∠BAC+∠BDC=180°,可证∠ABD=∠ACE,易证△ABD≌△ACE,得出△ADE是等边三角形,所以AD=DE,从而解决问题.
根据上述解题思路,三条线段DA、DB、DC之间的等量关系是;(直接写出结果)
(2)如图2,Rt△ABC中,∠BAC=90°,AB=AC.点D是边BC下方一点,∠BDC=90°,探索三条线段DA、DB、DC之间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地之间的路程为2380米,甲、乙两人分别从A、B两地出发,相向而行,已知甲先出发5分钟后,乙才出发,他们两人在A、B之间的C地相遇,相遇后,甲立即返回A地,乙继续向A地前行.甲到达A地时停止行走,乙到达A地时也停止行走,在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则乙到达A地时,甲与A地相距的路程是米. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖西瓜千克数之间的关系如图所示,那么小李赚了_________.元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的网格中建立平面直角坐标系后,![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ;
;
(2)借助图中的网格,请只用直尺(不含刻度)完成以下要求:(友情提醒:请别忘了标注字母)
①在图中找一点![]() ,使得
,使得![]() 到边
到边![]() 的距离相等,且
的距离相等,且![]() ;
;
②在![]() 轴上找一点
轴上找一点![]() ,使得
,使得![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形![]() 的顶点
的顶点![]() 在坐标原点,顶点
在坐标原点,顶点![]() 分别在
分别在![]() 轴,
轴,![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 是边
是边![]() 上的一个动点,当
上的一个动点,当![]() 的周长最小时,点
的周长最小时,点![]() 的坐标为_________.
的坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.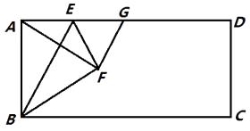
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示 ![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com