练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售，在销售了部分西瓜之后，余下的每千克降价0.4元，全部售完;销售金额与卖西瓜千克数之间的关系如图所示，那么小李赚了_________.元.

    【答案】36

    【解析】

    要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．

    由图中可知，没有降价前40千克西瓜卖了64元，那么售价为：64÷40=1.6元，

    降价0.4元后单价变为1.6-0.4=1.2，钱变成了76元，说明降价后卖了76-64=12元，那么降价后卖了12÷1.2=10千克，

    总质量将变为40+10=50千克，那么小李的成本为：50×0.8=40元，赚了76-40=36元，

    故答案为：36.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】设平面内一点到等边三角形中心的距离为d，等边三角形的内切圆半径为r，外接圆半径为R．对于一个点与等边三角形，给出如下定义：满足r≤d≤R的点叫做等边三角形的中心关联点． 在平面直角坐标系xOy中，等边△ABC的三个顶点的坐标分别为A（0，2），B（﹣ ，﹣1），C（ ，﹣1）．

    （1）已知点D（2，2），E（ ，1），F（﹣ ，﹣1）．在D，E，F中，是等边△ABC的中心关联点的是；
    （2）如图1，过点A作直线交x轴正半轴于M，使∠AMO=30°． ①若线段AM上存在等边△ABC的中心关联点P（m，n），求m的取值范围；
    ②将直线AM向下平移得到直线y=kx+b，当b满足什么条件时，直线y=kx+b上总存在等边△ABC的中心关联点；（直接写出答案，不需过程）
    （3）如图2，点Q为直线y=﹣1上一动点，⊙Q的半径为 ．当Q从点（﹣4，﹣1）出发，以每秒1个单位的速度向右移动，运动时间为t秒．是否存在某一时刻t，使得⊙Q上所有点都是等边△ABC的中心关联点？如果存在，请直接写出所有符合题意的t的值；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同，“春节期间”，两家采摘园将推出优惠方案，甲园的优惠方案是：游客进园需购买门票，采摘的草莓六折优惠；乙园的优惠方案是：游客进园不需购买门票，采摘园的草莓超过一定数量后，超过部分打折优惠．优惠期间，某游客的草莓采摘量为（千克），在甲园所需总费用为（元），在乙园所需总费用为（元），、与之间的函数关系如图所示，折线OAB表示与之间的函数关系．

    （1）甲采摘园的门票是 元，两个采摘园优惠前的草莓单价是每千克 元；

    （2）当＞10时，求与的函数表达式；

    （3）游客在“春节期间”采摘多少千克草莓时，甲、乙两家采摘园的总费用相同．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若数a使关于x的分式方程 + =4的解为正数，且使关于y的不等式组 的解集为y＜﹣2，则符合条件的所有整数a的和为（ ）
    A.10
    B.12
    C.14
    D.16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等边△ABC中，

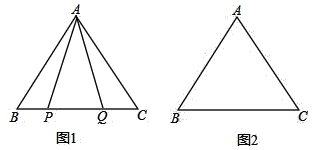
    （1）如图1，P，Q是BC边上两点，AP=AQ，∠BAP=20°，求∠AQB的度数；

    （2）点P，Q是BC边上的两个动点（不与点B，C重合），点P在点Q的左侧，且AP=AQ，点Q关于直线AC的对称点为M，连接AM，PM.

    ①依题意将图2补全；②小明通过观察、实验，提出猜想：在点P，Q运动的过程中，始终有PA=PM，小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：要证PA=PM，只需证△APM是等边三角形．

    想法2：在BA上取一点N，使得BN=BP，要证PA=PM，只需证△ANP≌△PCM.……

    请你参考上面的想法，帮助小明证明PA=PM（一种方法即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠ABM=45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．
    （1）如图1，若AB=3 ，BC=5，求AC的长；
    （2）如图2，点D是线段AM上一点，MD=MC，点E是△ABC外一点，EC=AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF=∠CEF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数据1，3，5，12，a，其中整数a是这组数据的中位数，则该组数据的平均数是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】销售有限公司到某汽车制造有限公司选购A、B两种型号的轿车，用300万元可购进A型轿车10辆，B型轿车15辆；用300万元可购进A型轿车8辆，B型轿车18辆.

    (1)求A、B两种型号的轿车每辆分别多少元？

    (2)若该汽车销售公司销售一辆A型轿车可获利8000元，销售一辆B型轿车可获利5000元，该汽车销售公司准备用不超过400万元购进A、B两种型号轿车共30辆，且这两种轿车全部售出后总获利不低于20.4万元，问：有几种购车方案？在这几种购车方案中，哪种获利最多？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

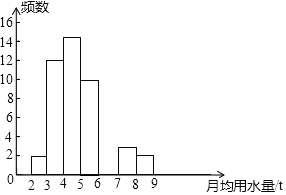
    【题目】小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了若干居民的月均用水量（单位：t），并绘制了不完整的样本的频数分布表的频数分布直方图（如图）

    根据上述图表回答下列问题：

    月均用水量（单位：t）

    频数

    百分比

    2≤x＜3

    2

    0.04

    3≤x＜4

    12

    0.24

    4≤x＜5

    5≤x＜6

    10

    0.2

    6≤x＜7

    0.12

    7≤x＜8

    3

    0.06

    8≤x＜9

    2

    0.04

    (1)小明同学共调查了多少户居民的月均用水量；

    (2)请根据题中已有的信息补全频数分布表和频数分布直方图；

    (3)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的等用水量家庭大约有多少户？

    查看答案和解析>>

    同步练习册答案