
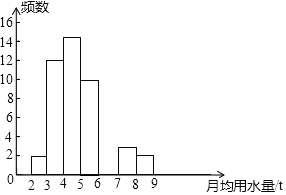
【题目】小明同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了若干居民的月均用水量(单位:t),并绘制了不完整的样本的频数分布表的频数分布直方图(如图)
根据上述图表回答下列问题:
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 0.04 |
3≤x<4 | 12 | 0.24 |
4≤x<5 | ||
5≤x<6 | 10 | 0.2 |
6≤x<7 | 0.12 | |
7≤x<8 | 3 | 0.06 |
8≤x<9 | 2 | 0.04 |
(1)小明同学共调查了多少户居民的月均用水量;
(2)请根据题中已有的信息补全频数分布表和频数分布直方图;
(3)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的等用水量家庭大约有多少户?
【答案】(1)小明同学共调查了50户居民的月均用水量;(2) 补全频数分布表见解析表格;补全频数分布直方图见解析;(3)通过样本估计总体中的等用水量家庭大约有279户.
【解析】
(1)根据第一组的频数是2,百分比是4%即可求得总人数;
(2)利用总户数50乘以6≤x<7的百分比可得其频数,再用总人数减去其余各组频数可得4≤x<5的频数及其频率;
(3)用4≤x<5、5≤x<6、6≤x<7的频率之和乘以总人数可得答案.
(1)调查的总数是:2÷0.04=50(户).
答:小明同学共调查了50户居民的月均用水量;
(2)因为共调查了50户,则6≤x<7部分调查的户数是:50×0.12=6(户),则4≤x<5的户数是:50﹣2﹣12﹣10﹣6﹣3﹣2=15(户),频率为:15÷50=0.3,补全频数分布表如下:
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 0.04 |
3≤x<4 | 12 | 0.24 |
4≤x<5 | 15 | 0.3 |
5≤x<6 | 10 | 0.2 |
6≤x<7 | 6 | 0.12 |
7≤x<8 | 3 | 0.06 |
8≤x<9 | 2 | 0.04 |
补全频数分布直方图如下:

(3)中等用水量家庭大约有450×(0.30+0.20+0.12)=279(户).
答:通过样本估计总体中的等用水量家庭大约有279户.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖西瓜千克数之间的关系如图所示,那么小李赚了_________.元.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,函数
,函数![]() 与
与![]() 的图像交于第四象限的点
的图像交于第四象限的点![]() ,且点
,且点![]() 的横坐标为1.
的横坐标为1.
(1)求![]() 的值;
的值;
(2)观察图像,当![]() 满足 时,
满足 时,![]() ;
;
(3)在![]() 轴上有一点
轴上有一点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交函数
轴的垂线,分别交函数![]() 和
和![]() 的图像于点
的图像于点![]() .若
.若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )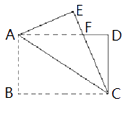
A. ![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.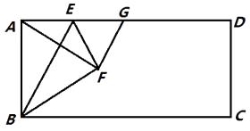
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示 ![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过抛物线y= ![]() x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
x2﹣2x上一点A作x轴的平行线,交抛物线于另一点B,交y轴于点C,已知点A的横坐标为﹣2.
(1)求抛物线的对称轴和点B的坐标;
(2)在AB上任取一点P,连结OP,作点C关于直线OP的对称点D;
①连结BD,求BD的最小值;
②当点D落在抛物线的对称轴上,且在x轴上方时,求直线PD的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外部相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为 ![]() ,则随机摸出一个红球的概率为( )
,则随机摸出一个红球的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com