
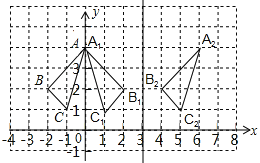
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

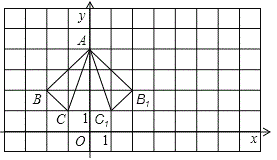
【答案】(1)如图,△A1B1C1即为所求,顶点C1的坐标为(1,1);
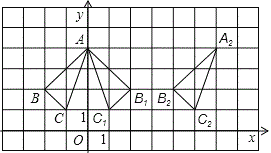
(2)如图,△A2B2C2即为所求,顶点C2的坐标为(5,1);
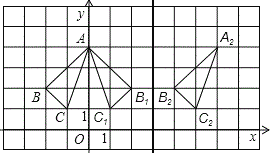
(3)△A1B1C1和△A2B2C2关于直线x=3对称如图:
【解析】
试题(1)根据轴对称的性质作出A、B、C关于y轴的对称点,A1、B1、C1,顺次连接画图,并找到坐标即可.(2)根据平移的性质将A、B、C按平移条件找出它的对应点A2、B2、C2,顺次连接画图,并找坐标即可.(3)观察图象即可得△A1B1C1和△A2B2C2,关于直线x=3对称.
试题解析:(1)如图,各顶点的坐标为:A1(0,4) B1 (2,2) C1(1,1);
(2)如图,各顶点的坐标为:A2 (6,4) B2 (4,2) C2(5,1);
(3)是关于某直线对称,对称轴是直线x=3.如图.


科目:初中数学 来源: 题型:
【题目】如图,在同一平面内四个点A,B,C,D.
(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.
①作射线AC;
②连接AB,BC,BD,线段BD与射线AC相交于点O;
③在线段AC上作一条线段CF,使CF=AC﹣BD.
(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是 .
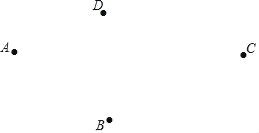
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角. 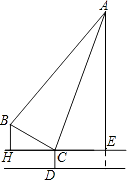
(1)求证:AB=AC
(2)求吊车的吊臂顶端A点距地面的高度是多少米?(保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,9). 
(1)画出△ABC,并求出AC所在直线的解析式.
(2)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1 , 并求出△ABC在上述旋转过程中扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
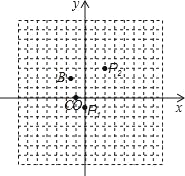
【题目】阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为(![]() ,
,![]() ).
).
观察应用:
(1)如图,在平面直角坐标系中,若点P1(0,﹣1)、P2(2,3)的对称中心是点A,则点A的坐标为 ;
(2)另取两点B(﹣1.6,2.1)、C(﹣1,0).有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…则点P3、P8的坐标分别为 、 .
拓展延伸:
(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论: ①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2 .
其中一定正确的是( )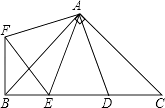
A.②④
B.①③
C.①④
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
【1】求证:△ABE≌△CDA;
【2】若∠DAC=40°,求∠EAC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com