
【题目】如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角. 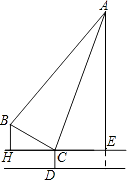
(1)求证:AB=AC
(2)求吊车的吊臂顶端A点距地面的高度是多少米?(保留根号)
【答案】
(1)证明:如图,∵∠BCH=30°,∠ACE=75°,
∴∠ACB=180°﹣∠BCH﹣∠ACE=75°,
∵∠ABC=75°,
∴∠ABC=∠BCA,
∴AB=AC
(2)解:作AL⊥BC于L,在AE上截取一点M,使得AM=MC.
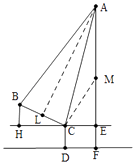
在△ACL和△ACE中,
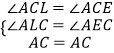 ,
,
∴△ACL≌△ACE,
∴CL=CE,
∵AB=AC,AL⊥BC,BC=4,
∴BL=CL=CE=2,
∵MA=MC,
∴∠MAC=∠MCA=90°﹣∠ACE=15°,
∴∠CME=30°,
∴CM=AM=2CE=4,ME=2 ![]() ,
,
∴AE=AM+ME=4+2 ![]() ,
,
∴AF=AE+EF=4+2 ![]() +2=6+2
+2=6+2 ![]() .
.
吊车的吊臂顶端A点距地面的高度是(6+2 ![]() )米.
)米.
【解析】(1)欲证明AB=AC,只要证明∠ABC=∠BCA即可.(2)作AL⊥BC于L,在AE上截取一点M,使得AM=MC.首先证明△ACL≌△ACE,得到CL=CE=2,只要证明∠CME=30°,求出CM,ME即可解决问题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
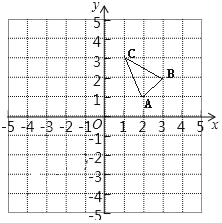
【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题:
(1)作出△ABC向左平移4个单位长度后得到的△A1B1C1,并写出点C1的坐标;
(2)将△A1B1C1绕原点O逆时针旋转90°得到△A2B2C2,请画出旋转后的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以O为圆心的弧 ![]() 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB. 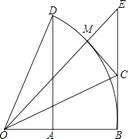
(1)求 ![]() 的值;
的值;
(2)若OE与 ![]() 交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D、均在小正方形的顶点上,请用无刻度直尺作出以下图形: 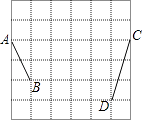
①在方格纸中画以AB为一边的菱形ABEF,点E、F在小正方形的顶点上,且菱形ABEF的面积为3;
②在方格纸中画以CD为一边的等腰△CDG,点G在小正方形的顶点上,连接EG,使∠BEG=90°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】烟台享有“苹果之乡”的美誉.甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果.甲超市销售方案是:将苹果按大小分类包装销售,其中大苹果400千克,以进价的2倍价格销售,剩下的小苹果以高于进价10%销售.乙超市的销售方案是:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利2100元(其它成本不计).问:
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个安装有进出水管的30升容器,水管单位时间内进出的水量是一定的,设从
某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,得到水量y(升)
与时间x(分)之间的函数关系如图所示.根据图象信息给出下列说法:

①每分钟进水5升;②当4≤x≤12时,容器中水量在减少;
③若12分钟后只放水,不进水,还要8分钟可以把水放完;
④若从一开始进出水管同时打开需要24分钟可以将容器灌满.
以上说法中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化学习环境,加强校园绿化建设,某校计划用不多于5200元的资金购买A、B两种树苗共60棵(可以是同一种树苗),加强校园绿化建设.若购买A种树苗x棵,所需总资金为y元,A、B两种树苗的相关信息如表:
项目 | 单价(元/棵) | 成活率 |
A | 100 | 98% |
B | 60 | 90% |
(1)求y与x之间的函数关系式;
(2)若要使得所购买树苗的成活率不低于95%,有几种选购方案?所用的资金分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com