
【题目】为了美化学习环境,加强校园绿化建设,某校计划用不多于5200元的资金购买A、B两种树苗共60棵(可以是同一种树苗),加强校园绿化建设.若购买A种树苗x棵,所需总资金为y元,A、B两种树苗的相关信息如表:
项目 | 单价(元/棵) | 成活率 |
A | 100 | 98% |
B | 60 | 90% |
(1)求y与x之间的函数关系式;
(2)若要使得所购买树苗的成活率不低于95%,有几种选购方案?所用的资金分别是多少?
【答案】
(1)解:y=100x+60(60﹣x)=40x+3600
100x+60(60﹣x)≤5200,
解得x≤40,
(∴0≤x≤40,且x为整数)
(2)解:98%x+90%(60﹣x)≥95%×60,
解得: ![]() ,
,
又∵x≤40,x是整数∴x=38、39、40.
所以有三种购树苗方案:①购A种树苗38棵、B种树苗22棵,所用资金38×100+22×60=5120元;②购A种树苗39棵、B种树苗21棵,所用资金39×100+21×60=5160元;③购A种树苗40棵、B种树苗20棵,所用资金为40×100+20×60=5200元
【解析】(1)总资金y=A树苗所需要的资金+B树苗所需要的资金;(2)关系式为:A种树木的成活数量+B种树木的成活数量≥树苗总数×95%,结合(1)中得到的自变量取值即可得到相应的选购方案及所用资金.


科目:初中数学 来源: 题型:
【题目】如图,分别是吊车在吊一物品时的示意图,已知吊车底盘CD的高度为2米,支架BC的长为4米,且与地面成30°角,吊绳AB与支架BC的夹角为75°,吊臂AC与地面成75°角. 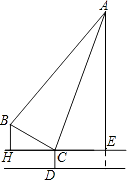
(1)求证:AB=AC
(2)求吊车的吊臂顶端A点距地面的高度是多少米?(保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
我们知道,任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1)、Q(x2,y2)的对称中心的坐标为(![]() ,
,![]() ).
).
观察应用:
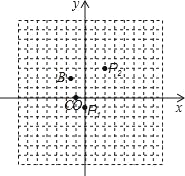
(1)如图,在平面直角坐标系中,若点P1(0,﹣1)、P2(2,3)的对称中心是点A,则点A的坐标为 ;
(2)另取两点B(﹣1.6,2.1)、C(﹣1,0).有一电子青蛙从点P1处开始依次关于点A、B、C作循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…则点P3、P8的坐标分别为 、 .
拓展延伸:
(3)求出点P2012的坐标,并直接写出在x轴上与点P2012、点C构成等腰三角形的点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论: ①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2 .
其中一定正确的是( )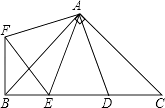
A.②④
B.①③
C.①④
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于函数y= ![]() ,下列说法中错误的是( )
,下列说法中错误的是( )
A.当x>0时,y随x的增大而增大
B.当x<0时,y随x的增大而增大
C.当x=1时的函数值大于x=﹣1时的函数值
D.在函数图象所在的每个象限内,y都随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,调查方式选择不合理的是![]()
![]()
A. 调查我国中小学生观看电影![]() 厉害了,我的国
厉害了,我的国![]() 情况,采用抽样调查的方式
情况,采用抽样调查的方式
B. 调查全市居民对“老年餐车进社区”活动的满意程度,采用抽样调查的方式
C. 调查“神州十一号”运载火箭发射前零部件质量状况,采用全面调查![]() 普查
普查![]() 的方式
的方式
D. 调查市场上一批LED节能灯的使用寿命,采用全面调查![]() 普查
普查![]() 的方式
的方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,已知AD∥BC,AB=CD,延长线段CB到E,使BE=AD,连接AE、AC.
【1】求证:△ABE≌△CDA;
【2】若∠DAC=40°,求∠EAC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论: ①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com