
【题目】在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4),C(﹣2,9). 
(1)画出△ABC,并求出AC所在直线的解析式.
(2)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1 , 并求出△ABC在上述旋转过程中扫过的面积.
【答案】
(1)解:如图所示,△ABC即为所求,
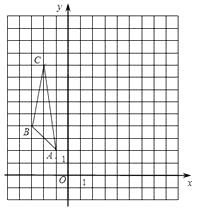
设AC所在直线的解析式为y=kx+b(k≠0),
∵A(﹣1,2),C(﹣2,9),
∴ ![]() ,
,
解得 ![]() ,
,
∴y=﹣7x﹣5
(2)解:如图所示,△A1B1C1即为所求,
由图可知, ![]() ,
,
S=S扇形+S△ABC,
= ![]() +2×7﹣1×5×
+2×7﹣1×5× ![]() ﹣1×7×
﹣1×7× ![]() ﹣2×2×
﹣2×2× ![]() ,
,
= ![]() .
.
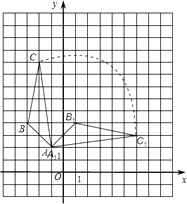
【解析】(1)利用待定系数法将A(﹣1,2),C(﹣2,9)代入解析式求出一次函数解析式即可;(2)根据AC的长度,求出S=S扇形+S△ABC , 就即可得出答案.
【考点精析】本题主要考查了确定一次函数的表达式和扇形面积计算公式的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,求跑步机手柄的一端A的高度h(精确到0.1m). (参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)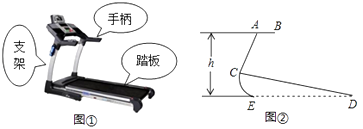
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展课外体育活动,决定开设![]() :篮球、
:篮球、![]() :乒乓球、
:乒乓球、![]() :踢毽子、
:踢毽子、![]() :跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
:跑步四种活动项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
(1)求出“最喜欢篮球”部分的扇形的圆心角度数;
(2)请把条形统计图补充完整;
(3)若该校有学生1000人,请根据样本估计全校最喜欢踢毽子的学生人数约是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点的坐标为(0,4),B点的坐标为(3,0),C(a,b)为平面直角坐标系内一点,若∠ABC=90°,且BA=BC,求ab的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com