
����Ŀ��ijѧУ��չ�������������������![]() :����
:����![]() :ƹ����
:ƹ����![]() :����ӡ�
:����ӡ�![]() :�ܲ����ֻ��Ŀ.Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ(ÿ��ֻѡȡһ��)�������ȡ�˲���ѧ�����е��飬���������������ס�����ʾ��ͳ��ͼ��������ͼ����Ϣ�����������.
:�ܲ����ֻ��Ŀ.Ϊ�˽�ѧ����ϲ����һ�ֻ��Ŀ(ÿ��ֻѡȡһ��)�������ȡ�˲���ѧ�����е��飬���������������ס�����ʾ��ͳ��ͼ��������ͼ����Ϣ�����������.
(1)�������ϲ�������ֵ����ε�Բ�ĽǶ�����
(2)�������ͳ��ͼ����������
(3)����У��ѧ��1000�ˣ��������������ȫУ��ϲ������ӵ�ѧ������Լ�Ƕ���?

���𰸡���1��![]() ��2����������3��100��
��2����������3��100��
��������
��1������100%��ȥD��C��B��������ռ�ٷֱȼ��ɵõ���ϲ��A��Ŀ��������ռ�İٷֱȣ���������ͳ��ͼ�ж�Ӧ��Բ�ĽǶ�����360���40%���ɣ�
��2������Ƶ��=�������ٷֱȿ��������������������������ȥD��C��B�����ֵ��������ɵõ�A���ֵ��������ٲ�ȫͼ�μ��ɣ�
��3����������������ÿ����ķ�����1000��������ϲ������ӵ�������ռ�ٷֱȼ��ɣ�
��1��100%-20%-10%-30%=40%��
360���40%=144�㣻
��2������ѧ����������15��30%=50��
50-15-5-10=20���ˣ�����ͼ��ʾ��
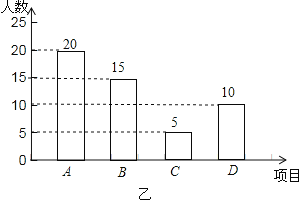
��3��1000��10%=100���ˣ���
��ȫУ��ϲ������ӵ�ѧ������Լ��100�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒÿ���ijɱ�Ϊ10Ԫ����������ÿ����Ʒ�������ۼ�x��Ԫ�����Ʒ����������y������֮��Ĺ�ϵ���±���
X��Ԫ�� | 15 | 20 | 25 | �� |
Y������ | 25 | 20 | 15 | �� |
��1���۲������y��x�ĺ�����ϵ����˵�����ɣ�
��2���������ۼ۶�Ϊ30Ԫʱÿ�յ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪��ABC�������������ֱ�ΪA����1��2����B����3��4����C����2��9���� 
��1��������ABC�������AC����ֱ�ߵĽ���ʽ��
��2��������ABC�Ƶ�A˳ʱ����ת90���õ��ġ�A1B1C1 �� �������ABC��������ת������ɨ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺
����֪������������������������߶ε��е�����ĶԳƣ���ƽ��ֱ������ϵ�У���������P��x1��y1����Q��x2��y2���ĶԳ����ĵ�����Ϊ(![]() ,
,![]() )��
)��
�۲�Ӧ�ã�
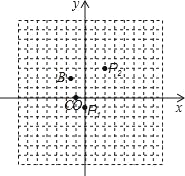
��1����ͼ����ƽ��ֱ������ϵ�У�����P1��0����1����P2��2��3���ĶԳ������ǵ�A�����A������Ϊ�� ����
��2����ȡ����B����1.6��2.1����C����1��0������һ�������ܴӵ�P1����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ��������P1���ڵ�A�ĶԳƵ�P2��������������P2���ڵ�B�ĶԳƵ�P3������������������P3���ڵ�C�ĶԳƵ�P4�������Ĵ���������P4���ڵ�A�ĶԳƵ�P5���������P3��P8������ֱ�Ϊ�� ������ ����
��չ���죺
��3�������P2012�����꣬��ֱ��д����x�������P2012����C���ɵ��������εĵ�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Ҫ�Ӽס���������Զ�˶�Ա����ѡһ�˲μ�У�˶���������������10��ѡ�����У����ǵijɼ����£���λ��cm����
�� | 585 | 596 | 610 | 598 | 612 | 597 | 604 | 600 | 613 | 601 |
�� | 613 | 618 | 580 | 574 | 618 | 593 | 585 | 590 | 598 | 624 |
��1�����ǵ�ƽ���ɼ��ֱ��Ƕ��٣�
��2���ס��������˶�Ա��10�α����ɼ��ļ������ֱ��Ƕ��٣�
��3�����������������˶�Ա���˶��ɼ���
��4����������������ɼ��ﵽ5.96m���п��ܶ�ڣ�����ΪΪ�˶��Ӧѡ��˭�μ���������������������ɼ��������ɼ��ﵽ6.10m���ܴ��Ƽ�¼����ô����ΪΪ�˴��Ƽ�¼Ӧѡ��˭�μ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У�AB=AC��D��E��б��BC�����㣬�ҡ�DAE=45�㣬����ADC�Ƶ�A˳ʱ����ת90��õ���AFB������EF�����н��ۣ� �١�AED�ա�AEF��
�ڡ�ABE�ס�ACD��
��BE+DC=DE��
��BE2+DC2=DE2 ��
����һ����ȷ���ǣ� ��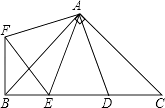
A.�ڢ�
B.�٢�
C.�٢�
D.�ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ں���y= ![]() ������˵���д�����ǣ� ��
������˵���д�����ǣ� ��
A.��x��0ʱ��y��x�����������
B.��x��0ʱ��y��x�����������
C.��x=1ʱ�ĺ���ֵ����x=��1ʱ�ĺ���ֵ
D.�ں���ͼ�����ڵ�ÿ�������ڣ�y����x�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�ACƽ�֡�BAD����C��CE��AB��E������AE��![]() (AB��AD)�����ABC����ADC�Ķ�����
(AB��AD)�����ABC����ADC�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com