
【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R.对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点. 在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣ ![]() ,﹣1),C(
,﹣1),C( ![]() ,﹣1).
,﹣1).
(1)已知点D(2,2),E( ![]() ,1),F(﹣
,1),F(﹣ ![]() ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是;
(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°. ①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为 ![]() .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
【答案】
(1)E、F
(2)①解:如图1中,由题意A(0,2),M( ![]() ,0).
,0).
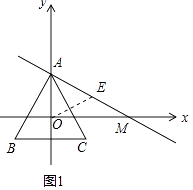
可求得直线AM的解析式为 ![]() .
.
经验证E在直线AM上.
因为OE=OA=2,∠MAO=60°,
所以△OAE为等边三角形,
所以AE边上的高长为 ![]() .
.
当点P在AE上时, ![]() ≤OP≤2.
≤OP≤2.
所以当点P在AE上时,点P都是等边△ABC的中心关联点.
所以0≤m≤ ![]() ;
;
②如图1﹣1中,设平移后的直线交y轴于G,作这条直线的垂线垂足为H.
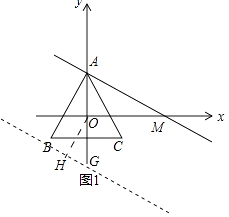
当OH=2时,在Rt△OHG中,∵OH=2,∠HOG=30°,
∴cos30°= ![]() ,
,
∴OG= ![]() ,
,
∴满足条件的b的值为﹣ ![]() ≤b≤2;
≤b≤2;
(3)存在.理由:如图2中,设Q(m,﹣1).

由题意当OQ= ![]() 时,⊙Q上所有点都是等边△ABC的中心关联点,
时,⊙Q上所有点都是等边△ABC的中心关联点,
![]() =
= ![]() ,
,
解得m= ![]() ,
,
∴t= ![]()
【解析】解:(1)由题意R=2,r=1,点O是△ABC的中心, ∵OD=2 ![]() ,OE=2,OF=
,OE=2,OF= ![]() ,
,
∴点E、F是△ABC的中心关联点
故答案为E,F;
(1)根据中心关联点,求出R、r、d即可判断;(2)①由题意可知,点E在直线AM上,当点P在AE上时,点P都是等边△ABC的中心关联点;②如图1﹣1中,设平移后的直线交y轴于G,作这条直线的垂线垂足为H.当OH=2时,求出OG即可判断;(3)存在.理由:如图2中,设Q(m,﹣1).由题意当OQ= ![]() 时,⊙Q上所有点都是等边△ABC的中心关联点,理由两点间距离公式即可求解.
时,⊙Q上所有点都是等边△ABC的中心关联点,理由两点间距离公式即可求解.


科目:初中数学 来源: 题型:
【题目】一元二次方程指:含有一个未知数,且未知数的最高次数为2的等式,求一元二次方程![]() 解的方法如下:第一步:先将等式左边关于x的项进行配方,
解的方法如下:第一步:先将等式左边关于x的项进行配方, ![]() ,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,
,第二步:配出的平方式保留在等式左边,其余部分移到等式右边,![]() ;第三步:根据平方的逆运算,求出
;第三步:根据平方的逆运算,求出![]() 或-3;第四步:求出
或-3;第四步:求出![]() .类比上述求一元二次方程根的方法,(1)解一元二次方程:
.类比上述求一元二次方程根的方法,(1)解一元二次方程:![]() ;
;
(2)求代数式![]() 的最小值;
的最小值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.
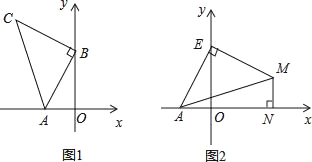
(1)求C点的坐标;
(2)在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;
(3)如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.
(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,P是BC上一点,E是AB上一点,PD平分∠APC,PE⊥PD,连接DE交AP于F,在以下判断中,不正确的是( )
A.当P为BC中点,△APD是等边三角形
B.当△ADE∽△BPE时,P为BC中点
C.当AE=2BE时,AP⊥DE
D.当△APD是等边三角形时,BE+CD=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)①画出△ABC关于y轴对称的△A1B1C1;
②画出△ABC绕点O按顺时针方向旋转90°后的△A2B2C2;
(2)判断△A1B1C1和△A2B2C2是不是成轴对称?如果是,请在图中作出它们的对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天内日销售量(m件)与时间(第x天)满足一次函数关系,部分数据如下表:
时间(第x天) | 1 | 3 | 6 | 10 | … |
日销售量(m件) | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
时间(第x天) | 1≤x<50 | 50≤x≤90 |
销售价格(元/件) | x+60 | 100 |
(1)求m关于x的一次函数表达式;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品哪天的销售利润最大?最大利润是多少?【提示:每天销售利润=日销售量×(每件销售价格﹣每件成本)】
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完;销售金额与卖西瓜千克数之间的关系如图所示,那么小李赚了_________.元.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com