
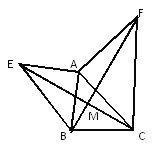
【题目】如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.求证:(1)EC=BF;(2)EC⊥BF.
【答案】见解析
【解析】
试题(1)先求出∠EAC=∠BAF,然后利用“边角边”证明△ABF和△AEC全等,根据全等三角形对应边相等即可证明;
(2)根据全等三角形对应角相等可得∠AEC=∠ABF,设AB、CE相交于点D,根据∠AEC+∠ADE=90°可得∠ABF+∠ADM=90°,再根据三角形内角和定理推出∠BMD=90°,从而得证.
证明:(1)∵AE⊥AB,AF⊥AC,
∴∠BAE=∠CAF=90°,
∴∠BAE+∠BAC=∠CAF+∠BAC,
即∠EAC=∠BAF,
在△ABF和△AEC中,
∵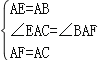 ,
,
∴△ABF≌△AEC(SAS),
∴EC=BF;
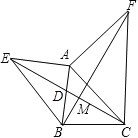
(2)如图,根据(1),△ABF≌△AEC,
∴∠AEC=∠ABF,
∵AE⊥AB,
∴∠BAE=90°,
∴∠AEC+∠ADE=90°,
∵∠ADE=∠BDM(对顶角相等),
∴∠ABF+∠BDM=90°,
在△BDM中,∠BMD=180°﹣∠ABF﹣∠BDM=180°﹣90°=90°,
所以EC⊥BF.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为 . 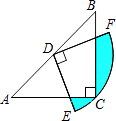
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大黄鱼是中国特有的地方性鱼种类,有“国鱼”之称.由于过去滥捕等多种因素,大黄鱼资源已基本枯竭.目前,我市已培育出十余种大黄鱼品种.某鱼苗人工养殖基地对其中的四个品种“宁港”、“御龙”、“甬岱”、“象山港”共300尾鱼苗进行成活实验,从中选出成活率最高的品种进行推广.通过实验得知“甬岱”品种鱼苗成活率为80%,并把实验数据绘制成下列两幅统计图(部分信息未给出):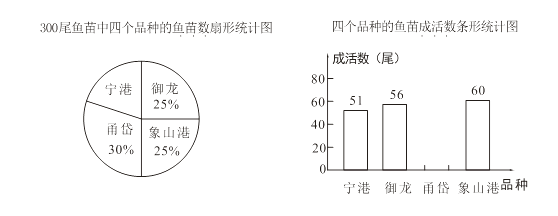
(1)求实验中“宁港”品种鱼苗的数量;
(2)求实验中“甬岱”品种鱼苗的成活数,并补全条形统计图;
(3)你认为应选哪一品种进行推广?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点 ![]() 出发,在矩形
出发,在矩形 ![]() 边上沿着
边上沿着 ![]() 的方向匀速移动,到达点
的方向匀速移动,到达点 ![]() 时停止移动.已知机器人的速度为
时停止移动.已知机器人的速度为 ![]() 个单位长度/
个单位长度/ ![]() ,移动至拐角处调整方向需要
,移动至拐角处调整方向需要 ![]()
![]() (即在
(即在 ![]() 、
、 ![]() 处拐弯时分别用时
处拐弯时分别用时 ![]()
![]() ).设机器人所用时间为
).设机器人所用时间为 ![]() 时,其所在位置用点
时,其所在位置用点 ![]() 表示,
表示, ![]() 到对角线
到对角线 ![]() 的距离(即垂线段
的距离(即垂线段 ![]() 的长)为
的长)为 ![]() 个单位长度,其中
个单位长度,其中 ![]() 与
与 ![]() 的函数图像如图②所示.
的函数图像如图②所示.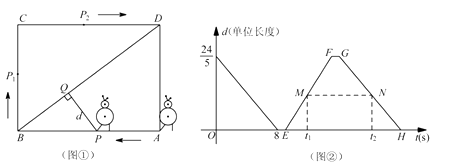
(1)求 ![]() 、
、 ![]() 的长;
的长;
(2)如图②,点 ![]() 、
、 ![]() 分别在线段
分别在线段 ![]() 、
、 ![]() 上,线段
上,线段 ![]() 平行于横轴,
平行于横轴, ![]() 、
、 ![]() 的横坐标分别为
的横坐标分别为 ![]() 、
、 ![]() .设机器人用了
.设机器人用了 ![]() 到达点
到达点 ![]() 处,用了
处,用了 ![]() 到达点
到达点 ![]() 处(见图①).若
处(见图①).若 ![]() ,求
,求 ![]() 、
、 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
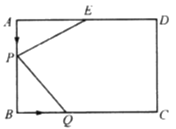
【题目】如图,在长方形![]() 中,
中,![]() cm,
cm,![]() cm,点
cm,点![]() 为
为![]() 的中点.若点
的中点.若点![]() 在线段
在线段![]() 上以1 cm/s的速度由点
上以1 cm/s的速度由点![]() 向点
向点![]() 运动,到点
运动,到点![]() 时不动.同时,点
时不动.同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.
运动.
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,经过1 s后,
的运动速度相等,经过1 s后,![]() 与
与![]() 是否全等?请说明理由,并判断此时线段
是否全等?请说明理由,并判断此时线段![]() 和
和![]() 的位置关系;
的位置关系;
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,运动时间为
的运动速度相等,运动时间为![]() s,设
s,设![]() 的面积为
的面积为![]() cm2,请用含
cm2,请用含![]() 的代数式表示
的代数式表示
(3)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,当点
的运动速度不相等,当点![]() 的运动速度为多少时,能够使
的运动速度为多少时,能够使![]() 与
与![]() 全等?
全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于 ![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 .
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为 . 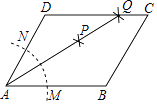
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.如图是某校三个年级学生人数分布的扇形统计图,其中八年级学生人数为408人,下表是该校学生阅读课外书籍情况统计表.根据图表中的信息,可知该校学生平均每人读课外书的本数是( )
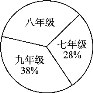
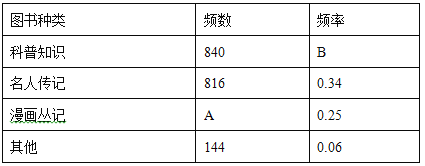
A. 2本 B. 3本 C. 4本 D. 5本
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com