Question

【题目】如图，四边形ABCD是某新建厂区示意图，∠A=75°，∠B=45°，BC⊥CD，AB=500 米，AD=200米，现在要在厂区四周建围墙，求围墙的长度有多少米？

Answer 1

【答案】解：如图，过点A作AE⊥BC于点E，过点D作DF⊥AE于点F，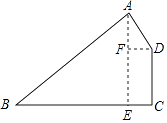

∵∠B=45°，
∴△ABE是等腰直角三角形，
∴AE=BE，∠BAE=∠B=45°．
∵AB=500 米，
∴AE=BE=500 × =500米．
∵∠A=75°，
∴∠DAF=75°﹣45°=30°．
∵AD=200米，
∴DF= AD=100米，AF=200× =100 米．
∵BC⊥CD，
∴四边形CDFE是矩形，
∴CD=EF=AE﹣AF=（500﹣100 ）米，CE=DF=100米，
∴AB+BC+AD+CD=500 +（500+100）+200+（500﹣100 ）=（1300+500 ﹣100 ）米．
答：围墙的长度是（1300+500 ﹣100 ）米．
【解析】过点A作AE⊥BC于点E，过点D作DF⊥AE于点F，根据∠B=45°可得出△ABE是等腰直角三角形，故可得出AE=BE，∠BAE=∠B=45°．再由∠A=75°可得出∠DAF的度数，进而可得出AF及DF的长，根据BC⊥CD可得出四边形CDFE是矩形，故可得出CD=EF，CE=DF，据此可得出结论．