
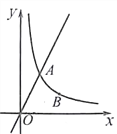
【题目】如图,直线y=2x与反比例函数![]() (k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(1)求k的值和点B坐标;
(2)若点P在x轴上,使得△PAB的面积为2,直接写出点P坐标。
【答案】(1)点B(2,1);(2) ![]() ,0)
,0) ![]() (7,0)
(7,0)
【解析】试题分析:(1)把点A(1,m)代入直线y=2x,就可得到点A的坐标,把点A的坐标代入反比例函数的解析式可得到k,再把点B的坐标代入反比例函数解析式,就可求出点B的坐标;
(2)延长AB交x轴于点C,先求出直线AB的解析式,从而得到点C的坐标.运用割补法可求出PC的值,结合点C的坐标就可求出m的值.
试题解析:解:∵点A是直线![]() 与双曲线
与双曲线![]() 的交点,∴m=2×1=2,∴点A(1,2),∴
的交点,∴m=2×1=2,∴点A(1,2),∴![]() ,解得:k=2.∵点B在双曲线
,解得:k=2.∵点B在双曲线![]() , ∴
, ∴![]() .∵
.∵![]() ,∴
,∴![]() .∵点B在第一象限,∴
.∵点B在第一象限,∴![]() ,
, ![]() , ∴点B(2,1).
, ∴点B(2,1).
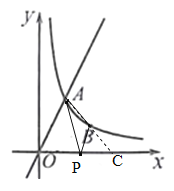
(2)延长AB交x轴于点C,如图2.设直线AB的解析式为:y=kx+b,则: ![]() ,解得:
,解得: ![]() ,∴直线AB为:y=-x+3,令y=0,得:x=3,∴C(3,0).∵S△PAB=2,∴S△PAB=S△PAC﹣S△PBC=
,∴直线AB为:y=-x+3,令y=0,得:x=3,∴C(3,0).∵S△PAB=2,∴S△PAB=S△PAC﹣S△PBC=![]() ×PC×2﹣
×PC×2﹣![]() ×PC×1=
×PC×1=![]() PC=2,∴PC=4.
PC=2,∴PC=4.
∵C(3,0),P(m,0),∴![]() =4,∴m=﹣1或7,∴P1(-1,0),P2(7,0).
=4,∴m=﹣1或7,∴P1(-1,0),P2(7,0).


 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
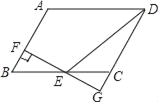
【题目】如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面表格给出了直线![]() 上部分点(x,y)的坐标值.
上部分点(x,y)的坐标值.
x | -2 | 0 | 2 | 4 |
y | 3 | 1 | -1 | -3 |
(1)直线![]() 与
与![]() 轴的交点坐标是___________;
轴的交点坐标是___________;
(2)直线![]() 与两坐标轴围成的三角形的面积等于___________.
与两坐标轴围成的三角形的面积等于___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民健身运动已成为一种时尚 ,为了解揭阳市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷内容包括五个项目:
A:健身房运动;B:跳广场舞;C:参加暴走团;D:散步;E:不运动.
以下是根据调查结果绘制的统计图表的一部分,
运动形式 | A | B | C | D | E |
人数 |
|
|
|
|
|
请你根据以上信息,回答下列问题:
![]() 接受问卷调查的共有 人,图表中的
接受问卷调查的共有 人,图表中的![]() ,
,![]() .
.
![]() 统计图中,
统计图中,![]() 类所对应的扇形的圆心角的度数是 度.
类所对应的扇形的圆心角的度数是 度.

![]() 揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有
揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有![]() 人,请你估计一下该社区参加环岛路“暴走团”的人数.
人,请你估计一下该社区参加环岛路“暴走团”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0)的图象过原点O和点A(1, ![]() ),且与x轴交于点B,△AOB的面积为
),且与x轴交于点B,△AOB的面积为![]() 。
。
(1)求抛物线的解析式;
(2)若抛物线的对称轴上存在一点M,使△AOM的周长最小,求M点的坐标;
(3)点F是x轴上一动点,过F作x轴的垂线,交直线AB于点E,交抛物线于点P,且PE=![]() ,直接写出点E的坐标(写出符合条件的两个点即可)。
,直接写出点E的坐标(写出符合条件的两个点即可)。


查看答案和解析>>
科目:初中数学 来源: 题型:
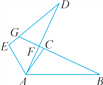
【题目】如图,△ABC≌△ADE,已知点C和点E是对应点,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应环保组织提出的“低碳生活”的号召,李明决定不开汽车而改骑自行车上班.有一天,李明骑自行车从家里到工厂上班,途中因自行车发生故障,修车耽误了一段时间,车修好后继续骑行,直至到达工厂(假设在骑自行车过程中匀速行驶).李明离家的距离![]() (米)与离家时间
(米)与离家时间![]() (分钟)的关系表示如下图:
(分钟)的关系表示如下图:
(1)李明从家出发到出现故障时的速度为 米/分钟;
(2)李明修车用时 分钟;
(3)求线段BC所对应的函数关系式(不要求写出自变量的取值范围).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com