
【题目】下面表格给出了直线![]() 上部分点(x,y)的坐标值.
上部分点(x,y)的坐标值.
x | -2 | 0 | 2 | 4 |
y | 3 | 1 | -1 | -3 |
(1)直线![]() 与
与![]() 轴的交点坐标是___________;
轴的交点坐标是___________;
(2)直线![]() 与两坐标轴围成的三角形的面积等于___________.
与两坐标轴围成的三角形的面积等于___________.
【答案】(1)(0,1); (2)![]() .
.
【解析】
(1)根据y轴上的点的横坐标为0解答即可;
(2)设直线l1的解析式为y=kx+b,根据表格得出直线l1过点(0,1)、(2,﹣1),利用待定系数法求出直线l1的解析式,得出与x轴的交点坐标,进而求解即可.
(1)由表1可知,当x=0时,y=1,
所以,直线l1与y轴的交点坐标是(0,1).
故答案为(0,1);
(2)设直线l1的解析式为y=kx+b,
∵直线l1过点(0,1)、(2,﹣1),
∴![]() ,解得
,解得![]() ,
,
∴直线l1的解析式为y=﹣x+1,
∵y=0时,x=1,
∴直线l1与x轴的交点坐标是(1,0),
∴直线l1与两坐标轴围成的三角形的面积等于![]() ×1×1=
×1×1=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到距A地18千米的B地,他们离开A地的距离![]() (千米)和行驶时间t(小时)之间的函数关系图象如图所示. 根据题目和图象提供的信息,下列说法正确的是( )
(千米)和行驶时间t(小时)之间的函数关系图象如图所示. 根据题目和图象提供的信息,下列说法正确的是( )
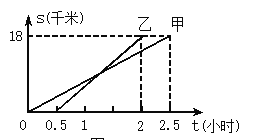
A. 乙比甲早出发半小时 B. 乙在行驶过程中没有追上甲
C. 乙比甲先到达B地 D. 甲的行驶速度比乙的行驶速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在□ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B-A-D-A运动,沿B-A运动时的速度为每秒13个单位长度,沿A-D-A运动时的速度为每秒8个单位长度.点Q从点 B出发沿BC方向运动,速度为每秒5个单位长度. P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A-D-A运动时,求AP的长(用含t的代数式表示).
(2) 当点P与点D重合时,求t的值
(3)连结AQ,在点P沿B-A-D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是两张不同类型火车的车票:(“D×××次”表示动车,“G×××次”表示高铁):
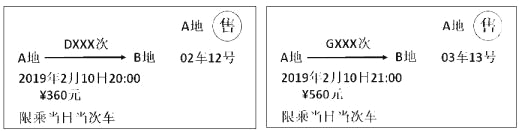
(1)根据车票中的信息填空:两车行驶方向 ,出发时刻 (填“相同”或“不同”);
(2)已知该动车和高铁的平均速度分别为200km/h,300km/h,如果两车均按车票信息准时出发,且同时到达终点,求A,B两地之间的距离;
(3)在(2)的条件下,请求出在什么时刻两车相距100km?
查看答案和解析>>
科目:初中数学 来源: 题型:
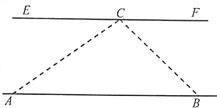
【题目】如图,湛河两岸AB与EF平行,小亮同学假期在湛河边A点处,测得对岸河边C处视线与湛河岸的夹角∠CAB=37°,沿河岸前行140米到点B处,测得对岸C处的视线与湛河岸夹角∠CBA=45°.问湛河的宽度约多少米?(参考数据:sin37°≈0.60,cos37°=0.80,tan37°=0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
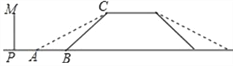
【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:![]() .
.
(1)求新坡面的坡角∠CAB的度数;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
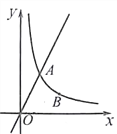
【题目】如图,直线y=2x与反比例函数![]() (k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(k≠0,x>0)的图象交于点A(1,m),点B(n,t)是反比例函数图象上一点,且n=2t。
(1)求k的值和点B坐标;
(2)若点P在x轴上,使得△PAB的面积为2,直接写出点P坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)1+(﹣1)+4﹣4
(2)﹣![]() ﹣(1﹣0.5)×
﹣(1﹣0.5)×![]() ×[1﹣(﹣2)2]
×[1﹣(﹣2)2]
(3)3x2y+xy2﹣3x2y﹣7xy2
(4)(5a﹣3b)﹣3(a﹣2b)
查看答案和解析>>
科目:初中数学 来源: 题型:
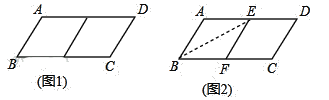
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是_______阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com