
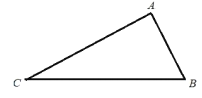
ЁОЬтФПЁПШчЭМ(1), вбжЊЁїABCжа, ЁЯBAC=900, AB=AC, AEЪЧЙ§AЕФвЛЬѕжБЯп, ЧвB.CдкA.EЕФвьВр, BDЁЭAEгкD, CEЁЭAEгкE
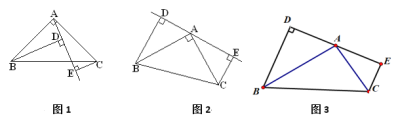
(1)ЪдЫЕУї: BD=DE+CE.
(2)ШєжБЯпAEШЦAЕуа§зЊЕНЭМ(2)ЮЛжУЪБ, ЦфгрЬѕМўВЛБф, ЮЪBDгыDE.CEЕФЪ§СПЙиЯЕШчКЮ?ЧыжБНгаДГіНсЙћ, ВЛашЫЕУї
(3)ШчЭМ(3)ШєНЋЭМЃЈ2ЃЉжаЕФAB=ACИФЮЊЁЯABD=ЁЯABCЦфгрЬѕМўВЛБф, ЮЪADгыAEЕФЪ§СПЙиЯЕШчКЮ? ВЂЫЕУїРэгЩ.
ЁОД№АИЁПЃЈ1ЃЉBD=DE+CEЃЛЃЈ2ЃЉBD=DE-CEЃЛЃЈ3ЃЉAD=AE.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊРћгУAASХаЖЈЁїABDЁеЁїCAEЕУГіBD=AEЃЌAD=CEЃЌИљОнЕШСПДњЛЛМДПЩЕУГі.
ЃЈ2ЃЉИљОнвбжЊРћгУAASХаЖЈЁїABDЁеЁїCAEДгЖјЕУЕНBD=AEЃЌAD=CEЃЌгЩAD+AE=BD+CEЃЌЕУГіBDЃЌDEЃЌCEжЎМфЕФЙиЯЕ.
ЃЈ3ЃЉзїAFЁЭBCгкЕуFЃЌЯШИљОнЁАAASЁБжЄУїЁїBADЁеЁїBAFЃЌдйИљОнЁАAASЁБжЄУїЁїCAEЁеЁїCAFЃЌМДПЩЕУЕНADгыAEЕФЪ§СПЙиЯЕ.
НтЃКЃЈ1ЃЉЁпЁЯBAC=90ЁуЃЌBDЁЭAEЃЌCEЁЭAEЃЌ
ЁрЁЯBDA=ЁЯAEC=90ЁуЃЌ
ЁпЁЯABD+ЁЯBAE=90ЁуЃЌЁЯCAE+ЁЯBAE=90Ёу
ЁрЁЯABD=ЁЯCAEЃЌ
ЁпAB=ACЃЌ
дкЁїABDКЭЁїCAEжаЃЌ
Ёп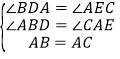 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрBD=AEЃЌAD=CEЃЌ
ЁпAE=AD+DEЃЌ
ЁрBD=DE+CEЃЛ
ЃЈ2ЃЉНсТлЃКBD=DE-CEЃЛ
ЁпЁЯBAC=90ЁуЃЌBDЁЭAEЃЌCEЁЭAEЃЌ
ЁрЁЯBDA=ЁЯAEC=90ЁуЃЌ
ЁрЁЯABD+ЁЯDAB=ЁЯDAB+ЁЯCAEЃЌ
ЁрЁЯABD=ЁЯCAEЃЌ
ЁпAB=ACЃЌ
дкЁїABDКЭЁїCAEжаЃЌ
Ёп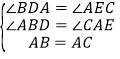 ЃЌ
ЃЌ
ЁрЁїABDЁеЁїCAEЃЈAASЃЉЃЌ
ЁрBD=AEЃЌAD=CEЃЌ
ЁрAD+AE=BD+CEЃЌ
ЁпDE=BD+CEЃЌ
ЁрBD=DE-CEЃЎ
ЃЈ3ЃЉзїAFЁЭBCгкЕуFЃЌ
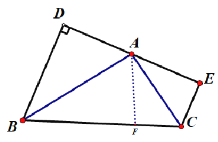
дкЁїBADКЭЁїBAFжаЃЌ
ЁпЁЯABD=ЁЯABCЃЌ
ЁЯD=ЁЯAFBЃЌ
AB=ABЃЌ
ЁрЁїBADЁеЁїBAFЃЌ
ЁрAD=AFЃЌЁЯBAD=ЁЯBAF.
ЁпЁЯCAE+ЁЯBAD=90Ёу, ЁЯCAF+ЁЯBAF=90Ёу,
ЁрЁЯCAE=ЁЯCAF.
дкЁїCAEКЭЁїCAFжаЃЌ
ЁпЁЯCAE=ЁЯCAFЃЌ
ЁЯE=ЁЯAFCЃЌ
AC=ACЃЌ
ЁрЁїCAEЁеЁїCAFЃЌ
ЁрAE=AFЃЌ
ЁрAD=AE.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЙћ10bЃНnЃЌФЧУДГЦbЮЊnЕФРЭИёЪ§ЃЌМЧЮЊbЃНdЃЈnЃЉЃЎ
ЃЈ1ЃЉИљОнРЭИёЪ§ЕФЖЈвхЃЌПЩжЊЃКdЃЈ10ЃЉЃН1ЃЌdЃЈ102ЃЉЃН2,ФЧУДЃКdЃЈ103ЃЉЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉРЭИёЪ§гаШчЯТдЫЫуаджЪЃКШєmЃЌnЮЊе§Ъ§ЃЌдђdЃЈmnЃЉЃНdЃЈmЃЉ+dЃЈnЃЉЃЛ dЃЈ![]() ЃЉЃНdЃЈmЃЉЉdЃЈnЃЉЃЎШєdЃЈ3ЃЉЃН0.48ЃЌdЃЈ2ЃЉЃН0.3ЃЌИљОндЫЫуаджЪЃЌЬюПеЃКdЃЈ6ЃЉЃНЁЁ ЁЁЃЌдђdЃЈ
ЃЉЃНdЃЈmЃЉЉdЃЈnЃЉЃЎШєdЃЈ3ЃЉЃН0.48ЃЌdЃЈ2ЃЉЃН0.3ЃЌИљОндЫЫуаджЪЃЌЬюПеЃКdЃЈ6ЃЉЃНЁЁ ЁЁЃЌдђdЃЈ![]() ЃЉЃНЁЁ ЁЁЃЌdЃЈ
ЃЉЃНЁЁ ЁЁЃЌdЃЈ![]() ЃЉЃНЁЁ ЁЁЃЎ
ЃЉЃНЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЋУёНЁЩэдЫЖЏвбГЩЮЊвЛжжЪБЩа ЃЌЮЊСЫНтНвбєЪаОгУёНЁЩэдЫЖЏЕФЧщПіЃЌФГНЁЩэЙнЕФЙЄзїШЫдБПЊеЙСЫвЛЯюЮЪОэЕїВщЃЌЮЪОэФкШнАќРЈЮхИіЯюФП:
A:НЁЩэЗПдЫЖЏЃЛB:ЬјЙуГЁЮшЃЛC:ВЮМгБЉзпЭХЃЛD:ЩЂВНЃЛE:ВЛдЫЖЏ.
вдЯТЪЧИљОнЕїВщНсЙћЛцжЦЕФЭГМЦЭМБэЕФвЛВПЗжЃЌ
дЫЖЏаЮЪН | A | B | C | D | E |
ШЫЪ§ |
|
|
|
|
|
ЧыФуИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬт:
![]() НгЪмЮЪОэЕїВщЕФЙВга ШЫЃЌЭМБэжаЕФ
НгЪмЮЪОэЕїВщЕФЙВга ШЫЃЌЭМБэжаЕФ![]() ЃЌ
ЃЌ![]() .
.
![]() ЭГМЦЭМжаЃЌ
ЭГМЦЭМжаЃЌ![]() РрЫљЖдгІЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ ЖШ.
РрЫљЖдгІЕФЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ ЖШ.

![]() НвбєЪаЛЗЕКТЗЪЧЪаУёЯВАЎЕФдЫЖЏГЁЫљжЎвЛЃЌУПЬьЖМгаЁАБЉзпЭХЁБЛюЖЏЃЌШєФГЩчЧјдМга
НвбєЪаЛЗЕКТЗЪЧЪаУёЯВАЎЕФдЫЖЏГЁЫљжЎвЛЃЌУПЬьЖМгаЁАБЉзпЭХЁБЛюЖЏЃЌШєФГЩчЧјдМга![]() ШЫЃЌЧыФуЙРМЦвЛЯТИУЩчЧјВЮМгЛЗЕКТЗЁАБЉзпЭХЁБЕФШЫЪ§.
ШЫЃЌЧыФуЙРМЦвЛЯТИУЩчЧјВЮМгЛЗЕКТЗЁАБЉзпЭХЁБЕФШЫЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
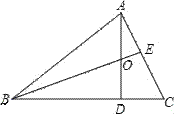
ЁОЬтФПЁПЁїABCжаЃЌADЁЭBCгкЕуDЃЌBEЪЧЁЯABCЕФЦНЗжЯпЃЌвбжЊЁЯABC=40ЁуЃЌЁЯC=60ЁуЃЌЧѓЁЯAOBЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
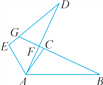
ЁОЬтФПЁПШчЭМЃЌЁїABCЁеЁїADEЃЌвбжЊЕуCКЭЕуEЪЧЖдгІЕуЃЌBCЕФбгГЄЯпЗжБ№НЛADЃЌDEгкЕуFЃЌGЃЌЧвЁЯDACЃН10ЁуЃЌЁЯBЃНЁЯDЃН25ЁуЃЌЁЯEABЃН120ЁуЃЌЪдЧѓЁЯDFBКЭЁЯDGBЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжжаЭКХЦћГЕгЭЯфШнСПЮЊ40LЃЌУПааЪЛ100kmКФгЭ10L.ЩшвЛСОМгТњгЭЕФИУаЭКХЦћГЕааЪЛТЗГЬЮЊxЃЈkmЃЉЃЌааЪЛЙ§ГЬжагЭЯфФкЪЃгргЭСПЮЊyЃЈLЃЉ
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЮЊСЫгааЇбгГЄЦћГЕЪЙгУЪйУќЃЌГЇМвНЈвщУПДЮМггЭЪБгЭЯфФкЪЃгргЭСПВЛЕЭгкгЭЯфШнСПЕФЫФЗжжЎвЛЃЌАДДЫНЈвщЃЌЧѓИУСОЦћГЕзюЖрааЪЛЕФТЗГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАжаЙњУЮЁБЙиЯЕУПИіШЫЕФавИЃЩњЛюЃЌЮЊеЙЯжЙуАВШЫзЗУЮЕФЗчВЩЃЌЮвЪаФГжабЇОйааЁАжаЙњУЮЮвЕФУЮЁБЕФбнНВБШШќЃЌШќКѓећРэВЮШќбЇЩњЕФГЩМЈЃЌНЋбЇЕФГЩМЈЗжЮЊAЃЌBЃЌCЃЌDЫФИіЕШМЖЃЌВЂНЋНсЙћЛцжЦГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЌЕЋОљВЛЭъећЃЌЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃЎ
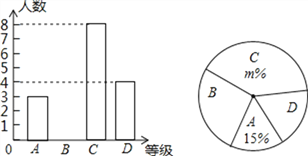
ЃЈ1ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉзщЮЏЛсОіЖЈДгБОДЮБШШќжаЛёЕУAЕШМЖЕФбЇЩњжаЃЌбЁГі2УћШЅВЮМгЪажабЇЩњбнНВБШШќЃЌвбжЊAЕШМЖжаФаЩњга1УћЃЌЧыгУЁАСаБэЁБЛђЁАЛЪїзДЭМЁБЕФЗНЗЈЧѓГіЫљбЁ2УћбЇЩњжаЧЁКУЪЧвЛУћФаЩњКЭвЛУћХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
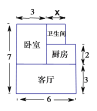
ЁОЬтФПЁПФГШЫзМБИЙКТђвЛЬзаЁЛЇаЭзЁЗПЃЌЫћШЅФГТЅХЬСЫНтЧщПіЕУжЊЃЌИУЛЇаЭЕЅМлЪЧ![]() дЊ/
дЊ/![]() ЃЌзмУцЛ§ШчЭМЫљЪОЃЈЕЅЮЛЃКУзЃЌЮРЩњМфЕФПэЮДЖЈЃЌЩшПэЮЊ
ЃЌзмУцЛ§ШчЭМЫљЪОЃЈЕЅЮЛЃКУзЃЌЮРЩњМфЕФПэЮДЖЈЃЌЩшПэЮЊ![]() УзЃЉЃЌЪлЗПВПЮЊЫћЬсЙЉСЫвдЯТСНжжгХЛнЗНАИЃК ЗНАИвЛЃКашЙКТђШЋВПзмУцЛ§ЃЌЕЋећЬзЗПАДдЯњЪлзмН№ЖюЕФ9елГіЪлЃЛ
УзЃЉЃЌЪлЗПВПЮЊЫћЬсЙЉСЫвдЯТСНжжгХЛнЗНАИЃК ЗНАИвЛЃКашЙКТђШЋВПзмУцЛ§ЃЌЕЋећЬзЗПАДдЯњЪлзмН№ЖюЕФ9елГіЪлЃЛ
ЗНАИЖўЃКећЬзЗПЕФЕЅМлШдЪЧ12000дЊ/![]() ЃЌЕЋВЛашвЊЙКТђШЋВПУцЛ§ЃЌЦфжаЃЌжЛЖдГјЗПУцЛ§НјааСЫгХЛнЃЌжЛЫуГјЗП
ЃЌЕЋВЛашвЊЙКТђШЋВПУцЛ§ЃЌЦфжаЃЌжЛЖдГјЗПУцЛ§НјааСЫгХЛнЃЌжЛЫуГјЗП![]() ЕФУцЛ§ЃЌЦфгрЗПМфУцЛ§ВЛБфЃЎ
ЕФУцЛ§ЃЌЦфгрЗПМфУцЛ§ВЛБфЃЎ
ЃЈ1ЃЉЧѓЮРЩњМфЕФУцЛ§ЃЛ
ЃЈ2ЃЉЧыЗжБ№ЧѓГіСНжжЗНАИЙКТђвЛЬзИУЛЇаЭЩЬЦЗЗПЕФзмН№ЖюЃЛ
ЃЈ3ЃЉЕБ1Ём![]() Ём2ЃЌЧв
Ём2ЃЌЧв![]() ЮЊећЪ§ЪБЃЌбЁФФжжЗНАИЙКТђвЛЬзИУЛЇаЭЩЬЦЗЗПЕФзмН№ЖюНЯЩйЃП
ЮЊећЪ§ЪБЃЌбЁФФжжЗНАИЙКТђвЛЬзИУЛЇаЭЩЬЦЗЗПЕФзмН№ЖюНЯЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШ§НЧаЮжНЦЌ![]() ЃЈШчЭМЃЉЃЌНЋжНЦЌелЕўЃЌЪЙЕу
ЃЈШчЭМЃЉЃЌНЋжНЦЌелЕўЃЌЪЙЕу![]() гыЕу
гыЕу![]() жиКЯЃЌелКлЗжБ№гыБп
жиКЯЃЌелКлЗжБ№гыБп![]() ЃЌ
ЃЌ![]() НЛгкЕу
НЛгкЕу![]() ЁЂ
ЁЂ![]() ЃЌЕу
ЃЌЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕуЮЊЕу
ЕФЖдГЦЕуЮЊЕу![]() ЃЌСЊНс
ЃЌСЊНс![]() ЃЎ
ЃЎ
ЃЈ1ЃЉИљОнЬтвтзїГіЭМаЮЃК
ЃЈ2ЃЉШчЙћ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШчЙћ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ8ЃЌЧѓ
ЕФУцЛ§ЮЊ8ЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com