
【题目】已知三角形纸片![]() (如图),将纸片折叠,使点
(如图),将纸片折叠,使点![]() 与点
与点![]() 重合,折痕分别与边
重合,折痕分别与边![]() ,
,![]() 交于点
交于点![]() 、
、![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,联结
,联结![]() .
.
(1)根据题意作出图形:
(2)如果![]() ,求
,求![]() 的度数;
的度数;
(3)如果![]() ,
,![]() 的面积为8,求
的面积为8,求![]() 的面积.
的面积.
【答案】(1)答案见解析;(2)![]() ;(3)16
;(3)16
【解析】
(1)根据题目所给的作法,按要求作出图形即可;
(2)根据折叠的性质并结合角的相关性质求出∠DEF度数,进而求出∠DEC度数即可;
(3)设△BED中BE边的高为m,由此可得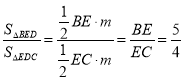 ,求出
,求出![]() 的面积;同理,设△AEC中EC边的高为n,据此可以得到:
的面积;同理,设△AEC中EC边的高为n,据此可以得到:![]() ,进一步计算即可得出答案.
,进一步计算即可得出答案.
如图所示:
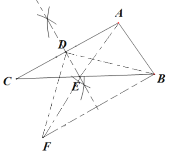
(2)∵![]() ,
,
∴2∠DEF=180°+50°=230°,
∴∠DEF=105°,
∴∠DEC=∠DEF-∠FEC=115°-50°=65°.
设△BED中BE边的高为m,
∴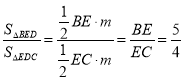 ,
,
∵由折叠性质可得:S△DEB=S△DEF=8,
∴![]() =
=![]() ,
,
∴![]() =2
=2![]() =
=![]() ,
,
设△AEC中EC边的高为n,
同理可得: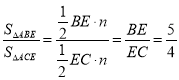 ,
,
∴![]() =
=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B.C在A.E的异侧, BD⊥AE于D, CE⊥AE于E
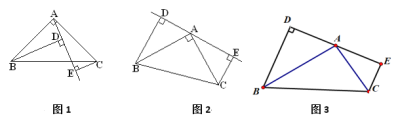
(1)试说明: BD=DE+CE.
(2)若直线AE绕A点旋转到图(2)位置时, 其余条件不变, 问BD与DE.CE的数量关系如何?请直接写出结果, 不需说明
(3)如图(3)若将图(2)中的AB=AC改为∠ABD=∠ABC其余条件不变, 问AD与AE的数量关系如何? 并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的正偶数2,4,6,8…,排成下表:
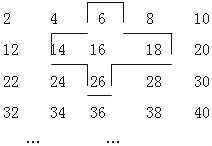
(1)十字框中的五个数的和是中间的数16的几倍?
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为![]() ,用代数式表示十字框中的五个数的和;
,用代数式表示十字框中的五个数的和;
(3)这五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图(1)中含“○”的矩形有1个,图(2)中含“○”的矩形有7个,图(3)中含“○”的矩形有17个,按此规律,图(6)中含“○”的矩形有( )
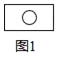
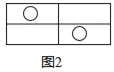
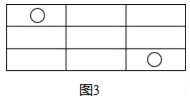
A. 70 B. 71 C. 72 D. 73
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=2x2﹣mx+m﹣2,以下结论:
①抛物线交x轴有交点;
②不论m取何值,抛物线总经过点(1,0);
③若m>6,抛物线交x轴于A、B两点,则AB>1;
④抛物线的顶点在y=﹣2(x﹣1)2图象上.其中正确的序号是( )
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人从A地出发前往B地,甲先出发1分钟后,乙再出发,乙出发一段时间后返回A地取物品,甲、乙两人同时达到B地和A地,并立即掉头相向而行直至相遇,甲、乙两人之间相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示,则甲、乙两人最后相遇时,乙距B地的路程是_____米.
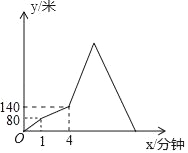
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材母题 点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S.
(1)用含有x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积为多少?
(3)△OPA的面积能大于24吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,∠ABC=60°,AB=4,AD=8,点E,F分别是边BC,AD的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是______.
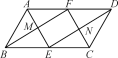
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA﹣AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是![]() cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
(1)用含x的代数式表示线段AP的长.
(2)当点P在线段BA上运动时,求y与x之间的函数关系式.
(3)当经过点B′和△ADC一个顶点的直线平分△ADC的面积时,直接写出x的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com