
【题目】如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA﹣AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是![]() cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
(1)用含x的代数式表示线段AP的长.
(2)当点P在线段BA上运动时,求y与x之间的函数关系式.
(3)当经过点B′和△ADC一个顶点的直线平分△ADC的面积时,直接写出x的值.

【答案】(1)当![]() 时,PA=5t,当1<x<5时,
时,PA=5t,当1<x<5时,![]()
(2)y=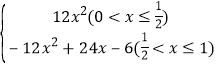 ;(3)x=
;(3)x=![]() s或
s或![]() s或
s或![]() s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积.
s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积.
【解析】分析:(1)分两种情形讨论即可.
(2)分两种情形①如图1中,当![]() 时,重叠部分是四边形PBQB′.
时,重叠部分是四边形PBQB′.
②如图2中,当![]() 重叠部分是五边形PBQMN.分别求解即可.
重叠部分是五边形PBQMN.分别求解即可.
(3)分三种情形①如图3中,当PA=B时,PB′是△ABD是中位线.②如图4中,设AB′的延长线交BC于G.③如图5中,连接DB′交AC于N,延长B′P交AD于T,作NM⊥PB′于M,NH⊥AD于H.分别构建方程即可解决问题.
详解:(1)当![]() 时,PA=5t,
时,PA=5t,
当1<x<5时,![]()
(2)如图1中,当![]() 时,重叠部分是四边形PBQB′.
时,重叠部分是四边形PBQB′.
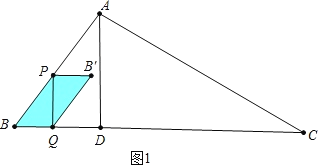
∵PQ⊥BC,AD⊥BC,
∴PQ∥AD,
∴![]()
∴![]()
∴PQ=4x,BQ=3x,
由题意四边形PBQB′是平行四边形,
∴![]()
如图2中,当![]() 重叠部分是五边形PBQMN.
重叠部分是五边形PBQMN.
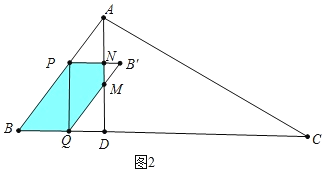
∵PN∥BD,
∴![]()
∴PN=3(1x),B′N=3x3(1x)=6x3,易知MN=4(2x
∴![]()
综上所述,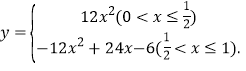
(3)如图3中,当PA=B时,PB′是△ABD是中位线。
∴AB′=DB′,此时CB′平分△ADC的面积,此时![]() .
.
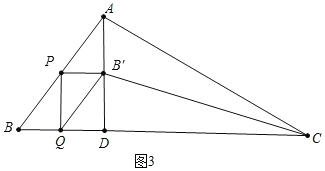
如图4中,设AB′的延长线交BC于G.
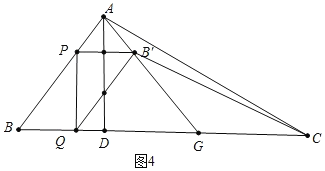
当DG=GC=4时,AB′平分△ADC的面积,
∵PB′∥BG,
∴![]() ∴
∴![]()
∴![]()
如图5中,连接DB′交AC于N,延长B′P交AD于T,作NM⊥PB′于M,NH⊥AD于H.
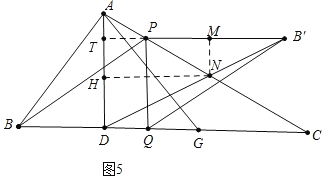
由题意PA=![]() (x1),AT=x1,TP=2(x1),PB′=BQ=3+2(x1)=2x+1,
(x1),AT=x1,TP=2(x1),PB′=BQ=3+2(x1)=2x+1,
当AN=CN时,DB′平分△ADC的面积,
∴可得AH=HD=2,HN=TM=2,
∴B′M=TB′MT=2(x1)+2x+14=4x5,MN=2(x1)=3x,TD=4(x1)=5x,
∵MN∥TD,
∴![]()
∴![]()
∴![]()
综上所述,x=![]() s或
s或![]() s或
s或![]() s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积。
s时,经过点B′和△ADC一个顶点的直线平分△ADC的面积。


科目:初中数学 来源: 题型:
【题目】已知三角形纸片![]() (如图),将纸片折叠,使点
(如图),将纸片折叠,使点![]() 与点
与点![]() 重合,折痕分别与边
重合,折痕分别与边![]() ,
,![]() 交于点
交于点![]() 、
、![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() ,联结
,联结![]() .
.
(1)根据题意作出图形:
(2)如果![]() ,求
,求![]() 的度数;
的度数;
(3)如果![]() ,
,![]() 的面积为8,求
的面积为8,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
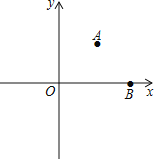
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD的度数为__________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形OABC放入平面直角坐标系xO中,使OA、OC分别落在x、y轴的正半轴上,其中AB=15,对角线AC所在直线解析式为y=﹣![]() x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.
x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.
(1)求点B的坐标;
(2)求EA的长度;
(3)点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)把下列各数分别填在相应的集合里:
![]() ,
,![]() ,
,![]() ,
,![]() ,0,
,0,![]() ,……
,……
正有理数集合:{ …}
整数集合:{ …}
分数集合:{ …}
(2)在下面的数轴上表示下列各数,并按照从小到大的顺序用“<”号连接起来
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地相距
两地相距![]() 千米,甲、乙两人都从
千米,甲、乙两人都从![]() 地去
地去![]() 地,图中
地,图中![]() 和
和![]() 分别表示甲、乙两人所走路程
分别表示甲、乙两人所走路程![]() (千米)与时间
(千米)与时间![]() (小时)之间的关系.对于下列说法:①乙晚出发
(小时)之间的关系.对于下列说法:①乙晚出发![]() 小时;②乙出发
小时;②乙出发![]() 小时后追上甲;③甲的速度是
小时后追上甲;③甲的速度是![]() 千米/小时;④乙先到达
千米/小时;④乙先到达![]() 地,其中正确的个数是( )
地,其中正确的个数是( )
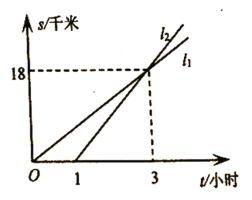
A.![]() 个B.3个C.2个D.1个
个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[材料阅读]
材料一:如图,![]() ,点
,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() ,点
,点![]() ,D分别在
,D分别在![]() 上.可求得如下结论:
上.可求得如下结论:![]() ,
,![]() 为定值.
为定值.
材料二(性质):四边形的内角和为![]() .
.
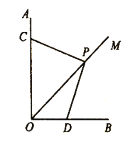
[问题解决]
(1)如图,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() 的边与
的边与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
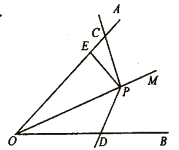
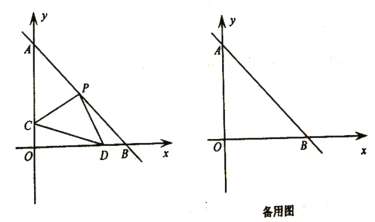
(2)如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,连接
,连接![]() .求
.求![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
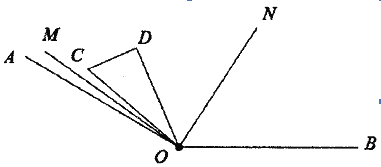
【题目】如图,已知![]() ,将一个直角三角形纸片(
,将一个直角三角形纸片(![]() )的一个顶点放在点
)的一个顶点放在点![]() 处,现将三角形纸片绕点
处,现将三角形纸片绕点![]() 任意转动,
任意转动,![]() 平分斜边
平分斜边![]() 与
与![]() 的夹角,
的夹角,![]() 平分
平分![]() .
.
(1)将三角形纸片绕点![]() 转动(三角形纸片始终保持在
转动(三角形纸片始终保持在![]() 的内部),若
的内部),若![]() ,则
,则![]() _______;
_______;
(2)将三角形纸片绕点![]() 转动(三角形纸片始终保持在
转动(三角形纸片始终保持在![]() 的内部),若射线
的内部),若射线![]() 恰好平方
恰好平方![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
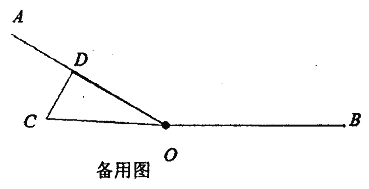
(3)将三角形纸片绕点![]() 从
从![]() 与
与![]() 重合位置逆时针转到
重合位置逆时针转到![]() 与
与![]() 重合的位置,猜想在转动过程中
重合的位置,猜想在转动过程中![]() 和
和![]() 的数量关系?并说明理由.
的数量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com