
【题目】[材料阅读]
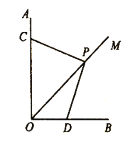
材料一:如图,![]() ,点
,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() ,点
,点![]() ,D分别在
,D分别在![]() 上.可求得如下结论:
上.可求得如下结论:![]() ,
,![]() 为定值.
为定值.
材料二(性质):四边形的内角和为![]() .
.
[问题解决]
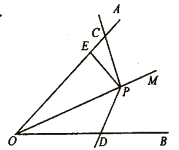
(1)如图,点![]() 在
在![]() 的平分线
的平分线![]() 上,
上,![]() 的边与
的边与![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
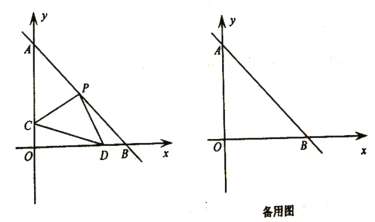
(2)如图,在平面直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 与
与![]() 轴的正半轴交于点
轴的正半轴交于点![]() ,连接
,连接![]() .求
.求![]() 的长度.
的长度.
【答案】(1)![]() ;(2)
;(2)![]() 的长度为
的长度为![]() 或
或![]()
【解析】
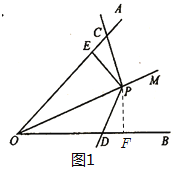
(1)如图1,作![]() 于点F,根据角平分线的性质可得PE=PF,再根据材料二的结论和已知条件可得∠OCP=∠FDP,进一步即可根据AAS证明
于点F,根据角平分线的性质可得PE=PF,再根据材料二的结论和已知条件可得∠OCP=∠FDP,进一步即可根据AAS证明![]() ,从而得
,从而得![]() ,由勾股定理易得
,由勾股定理易得![]() ,进而可推出
,进而可推出![]() ,而OE可根据勾股定理求出,于是可得结论;
,而OE可根据勾股定理求出,于是可得结论;
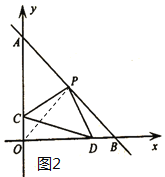
(2)分情况讨论:①若点C在线段AO上,由一次函数与坐标轴的交点可得OA=OB=7,可得△AOB是等腰直角三角形,如图2,连接![]() ,根据等腰直角三角形的性质和余角的性质可得OP=BP,∠PBO=∠POA =45°,∠OPC=∠BPD,进而可根据ASA证明
,根据等腰直角三角形的性质和余角的性质可得OP=BP,∠PBO=∠POA =45°,∠OPC=∠BPD,进而可根据ASA证明![]() ,可得
,可得![]() ,然后在
,然后在![]() 中利用勾股定理即可求出CD;
中利用勾股定理即可求出CD;
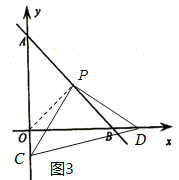
②若点C在射线AO上,如图3,连接![]() ,仿①的思路利用ASA证明
,仿①的思路利用ASA证明![]() ,可得
,可得![]() ,然后在
,然后在![]() 中利用勾股定理求解即可.
中利用勾股定理求解即可.
解:(1)如图1,作![]() 于点F,∵PO平分∠AOB,PE⊥OA,∴PE=PF,
于点F,∵PO平分∠AOB,PE⊥OA,∴PE=PF,
在四边形OCPD中,∵![]() ,∴由材料二的结论得:
,∴由材料二的结论得:![]() ,
,
∵![]() ,∴∠OCP=∠FDP,
,∴∠OCP=∠FDP,
在△PEC和△PFD中,∵∠OCP=∠FDP,∠CEP=∠DFP=90°,PE=PF,
∴![]() (AAS),∴
(AAS),∴![]() .
.
∵![]() ,PE=PF,∴
,PE=PF,∴![]() .
.
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ;
;
(2)分情况讨论:①若点C在线段AO上,由直线![]() ,可得
,可得![]() ,A(0,7),∴OA=OB=7,∴△AOB是等腰直角三角形,
,A(0,7),∴OA=OB=7,∴△AOB是等腰直角三角形,
如图2,连接![]() ,∵P为AB中点,∴OP=AP=BP,∠PBO=∠POC=∠POB=45°,∠OPB=90°,
,∵P为AB中点,∴OP=AP=BP,∠PBO=∠POC=∠POB=45°,∠OPB=90°,
∵![]() ,∴∠BPD+∠OPD=90°,
,∴∠BPD+∠OPD=90°,
∵∠OPC+∠OPD=90°,∴∠OPC=∠BPD,
∴![]() (ASA),∴
(ASA),∴![]() ,
,
又∵OB=7,∴OD=5,则在![]() 中,
中,![]() ;
;
②若点C在射线AO上,如图3,连接![]() ,
,
∵△AOB是等腰直角三角形,P为AB中点,
∴OP=BP,∠PBO=∠POA =45°,∠OPB=90°,
∴∠POC=∠PBD=135°,
又∵![]() ,∴∠BPD+∠CPB=90°,
,∴∠BPD+∠CPB=90°,
∵∠OPC+∠CPB=90°,∴∠OPC=∠BPD,
∴![]() (ASA),∴
(ASA),∴![]() ,
,
∵OB=7,∴![]() ,则在
,则在![]() 中,
中,![]() .
.
综上所述,![]() 的长度为
的长度为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
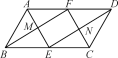
【题目】如图,ABCD中,∠ABC=60°,AB=4,AD=8,点E,F分别是边BC,AD的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA﹣AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是![]() cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
(1)用含x的代数式表示线段AP的长.
(2)当点P在线段BA上运动时,求y与x之间的函数关系式.
(3)当经过点B′和△ADC一个顶点的直线平分△ADC的面积时,直接写出x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
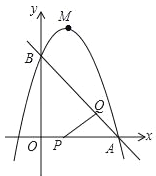
【题目】如图,已知直线y=﹣x+3与x轴、y轴分别交于A,B两点,抛物线y=﹣x2+bx+c经过A,B两点,点P在线段OA上,从点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以![]() 个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
(1)求抛物线的解析式;
(2)当t为何值时,△APQ为直角三角形;
(3)过点P作PE∥y轴,交AB于点E,过点Q作QF∥y轴,交抛物线于点F,连接EF,当EF∥PQ时,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
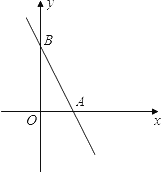
【题目】如图,直线![]() 与
与![]() 轴相交于点A,与
轴相交于点A,与![]() 轴相交于点B.
轴相交于点B.
(1)求A、B两点的坐标;
(2)求△AOB的面积;
(3)若点P是![]() 轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
轴上的一个动点,且△PAB是等腰三角形,则P点的坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
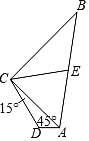
【题目】已知四边形ABCD中,AB=10,BC=8,CD=![]() ∠DAC=45°,∠DCA=15°.
∠DAC=45°,∠DCA=15°.
(1)求△ADC的面积;
(2)若E为AB的中点,求线段CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
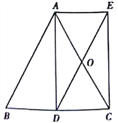
【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用三个正方形①、2个正方形②、1个正方形③和缺了一个角的长方形④,恰好拼成一个大长方形.根据图示数据,解答下列问题:
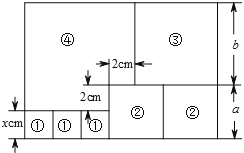
(1)用含x的代数式表示:a=__________cm,b=__________cm;
(2)用含x的代数式表示大长方形的周长,并求x=5时大长方形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新型节能环保汽车油箱中原有汽油100升,汽车每行驶50千米耗油8升,试写出汽车行驶的路程x(千米)与油箱中剩余油量y(升)之间的函数关系式,并画出这个函数的图象,函数的图象是什么形状?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com