
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ÷±œΏy=©¹x+3”κx÷αΓΔy÷αΖ÷±πΫΜ”ΎAΘ§BΝΫΒψΘ§≈ΉΈοœΏy=©¹x2+bx+cΨ≠ΙΐAΘ§BΝΫΒψΘ§ΒψP‘ΎœΏΕΈOA…œΘ§¥”ΒψA“‘1ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·ΘΜΆ§ ±Θ§ΒψQ‘ΎœΏΕΈAB…œΘ§¥”ΒψA≥ωΖΔΘ§œρΒψB“‘![]() ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·Θ§Ν§Ϋ”PQΘ§…η‘ΥΕ· ±ΦδΈΣtΟκΘ°
ΗωΒΞΈΜ/ΟκΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·Θ§Ν§Ϋ”PQΘ§…η‘ΥΕ· ±ΦδΈΣtΟκΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Β±tΈΣΚΈ÷Β ±Θ§ΓςAPQΈΣ÷±Ϋ«»ΐΫ«–ΈΘΜ
Θ®3Θ©ΙΐΒψPΉςPEΓΈy÷αΘ§ΫΜAB”ΎΒψEΘ§ΙΐΒψQΉςQFΓΈy÷αΘ§ΫΜ≈ΉΈοœΏ”ΎΒψFΘ§Ν§Ϋ”EFΘ§Β±EFΓΈPQ ±Θ§«σΒψFΒΡΉχ±ξΘ°
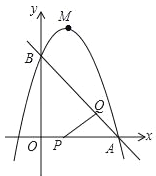

ΓΨ¥πΑΗΓΩΘ®1Θ©≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=©¹x2+2x+3ΘΜΘ®2Θ©Β±t=1Μρt=![]() ±Θ§ΓςPQA «÷±Ϋ«»ΐΫ«–ΈΘΜΘ®3Θ©ΒψFΒΡΉχ±ξΈΣΘ®2Θ§3Θ©Θ°
±Θ§ΓςPQA «÷±Ϋ«»ΐΫ«–ΈΘΜΘ®3Θ©ΒψFΒΡΉχ±ξΈΣΘ®2Θ§3Θ©Θ°
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©œ»άϊ”Ο÷±œΏΫβΈω Ϋ»ΖΕ®AΒψΚΆBΒψΉχ±ξΘ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©OP=tΘ§AQ=![]() tΘ§‘ρPA=3-tΘ§œ»≈–ΕœΓœQAP=45ΓψΘ§Χ÷¬έΘΚΒ±ΓœPQA=90Γψ ±Θ§»γΆΦΔΌΘ§άϊ”ΟΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟPA=
tΘ§‘ρPA=3-tΘ§œ»≈–ΕœΓœQAP=45ΓψΘ§Χ÷¬έΘΚΒ±ΓœPQA=90Γψ ±Θ§»γΆΦΔΌΘ§άϊ”ΟΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟPA=![]() AQΘ§Φ¥3-t=
AQȧ֥3-t=![]()
![]() tΘΜΒ±ΓœAPQ=90Γψ ±Θ§»γΆΦΔΎΘ§άϊ”ΟΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟAQ=
tΘΜΒ±ΓœAPQ=90Γψ ±Θ§»γΆΦΔΎΘ§άϊ”ΟΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ ΒΟAQ=![]() APΘ§Φ¥
APȧ֥![]() t=
t=![]() Θ®3-tΘ©Θ§»ΜΚσΖ÷±πΫβΙΊ”ΎtΒΡΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®3-tΘ©Θ§»ΜΚσΖ÷±πΫβΙΊ”ΎtΒΡΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®3Θ©»γΆΦΔέΘ§―”≥ΛFQΫΜx÷α”ΎΒψHΘ§…ηΒψPΒΡΉχ±ξΈΣΘ®tΘ§0Θ©Θ§‘ρΒψEΒΡΉχ±ξΈΣΘ®tΘ§-t+3Θ©Θ§“ΉΒΟΓςAQHΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§‘ρAH=HQ=![]() AQ=tΘ§‘ρΩ…±μ Ψ≥ωΒψQΒΡΉχ±ξΈΣΘ®3-tΘ§tΘ©Θ§ΒψFΒΡΉχ±ξΈΣ[3-tΘ§-Θ®3-tΘ©2+2Θ®3-tΘ©+3Θ©]Θ§Υυ“‘FQ=-t2+3tΘ§‘Ό÷ΛΟςΥΡ±Ώ–ΈPQFEΈΣΤΫ––ΥΡ±Ώ–ΈΒΟΒΫEP=FQΘ°Φ¥3-t=3t-t2Θ§»ΜΚσΫβΖΫ≥Χ«σ≥ωtΦ¥Ω…ΒΟΒΫΒψFΒΡΉχ±ξ.
AQ=tΘ§‘ρΩ…±μ Ψ≥ωΒψQΒΡΉχ±ξΈΣΘ®3-tΘ§tΘ©Θ§ΒψFΒΡΉχ±ξΈΣ[3-tΘ§-Θ®3-tΘ©2+2Θ®3-tΘ©+3Θ©]Θ§Υυ“‘FQ=-t2+3tΘ§‘Ό÷ΛΟςΥΡ±Ώ–ΈPQFEΈΣΤΫ––ΥΡ±Ώ–ΈΒΟΒΫEP=FQΘ°Φ¥3-t=3t-t2Θ§»ΜΚσΫβΖΫ≥Χ«σ≥ωtΦ¥Ω…ΒΟΒΫΒψFΒΡΉχ±ξ.
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏy=©¹x+3”κx÷αΫΜ”ΎΒψAΘ§”κy÷αΫΜ”ΎΒψBΘ§
ΓύΒ±y=0 ±Θ§x=3Θ§Φ¥AΒψΉχ±ξΈΣΘ®3Θ§0Θ©Θ§Β±x=0 ±Θ§y=3Θ§Φ¥BΒψΉχ±ξΈΣΘ®0Θ§3Θ©Θ°
ΓΏΫΪAΘ®3Θ§0Θ©Θ§BΘ®0Θ§3Θ©¥ζ»κΒΟΘΚ ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=©¹x2+2x+3Θ°
Θ®2Θ©ΓΏOA=OB=3Θ§ΓœBOA=90ΓψΘ§
ΓύΓœQAP=45ΓψΘ°
»γΆΦΔΌΥυ ΨΘΚΓœPQA=90Γψ ±Θ°
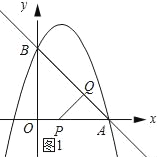
…η‘ΥΕ· ±ΦδΈΣtΟκΘ§‘ρQA=![]() tΘ§PA=3©¹tΘ°
tΘ§PA=3©¹tΘ°
‘ΎRtΓςPQA÷–Θ§ ![]() Θ§Φ¥
Θ§Φ¥![]() Θ°
Θ°
ΫβΒΟΘΚt=1Θ°
»γΆΦΔΎΥυ ΨΘΚΓœQPA=90Γψ ±Θ°
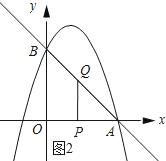
…η‘ΥΕ· ±ΦδΈΣtΟκΘ§‘ρQA=![]() tΘ§PA=3©¹tΘ°
tΘ§PA=3©¹tΘ°
‘ΎRtΓςPQA÷–Θ§ ![]() Θ§Φ¥
Θ§Φ¥![]() Θ°
Θ°
ΫβΒΟΘΚt=![]() Θ°
Θ°
Ήέ…œΥυ ωΘ§Β±t=1Μρt=![]() ±Θ§ΓςPQA «÷±Ϋ«»ΐΫ«–ΈΘ°
±Θ§ΓςPQA «÷±Ϋ«»ΐΫ«–ΈΘ°
Θ®3Θ©»γΆΦΔέΥυ ΨΘΚ
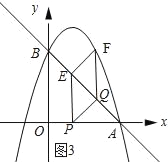
…ηΒψPΒΡΉχ±ξΈΣΘ®tΘ§0Θ©Θ§‘ρΒψEΒΡΉχ±ξΈΣΘ®tΘ§©¹t+3Θ©Θ§‘ρEP=3©¹tΘ°ΒψQΒΡΉχ±ξΈΣΘ®3©¹tΘ§tΘ©Θ§ΒψFΒΡΉχ±ξΈΣΘ®3©¹tΘ§©¹Θ®3©¹tΘ©2+2Θ®3©¹tΘ©+3Θ©Θ§Φ¥FΘ®3©¹tΘ§4t©¹t2Θ©Θ§‘ρFQ=4t©¹t2©¹t=3t©¹t2Θ°
ÿEPøFQȧEFøPQȧ
ΓύΥΡ±Ώ–ΈEFQPΈΣΤΫ––ΥΡ±Ώ–ΈΘ°
ΓύEP=FQΘ§Φ¥3©¹t=3t©¹t2Θ°
ΫβΒΟΘΚt1=1Θ§t2=3Θ®…α»ΞΘ©Θ°
ΫΪt=1¥ζ»κΒΟΒψFΒΡΉχ±ξΈΣΘ®2Θ§3Θ©Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΑ”÷Χπ”÷¥ύΓ±Υ°ΙϊΒξœ÷¥”≈ζΖΔ –≥Γ¬ρΫχ6œδΤΜΙϊΘ§¬ρΫχΦέΟΩœδ40‘ΣΘ§“‘ΟΩœδ![]() ΈΣΉΦΘ§≥Τ÷ΊΦ« Ψ»γœ¬Θ®≥§ΙΐΈΣ’ΐΘ§≤ΜΉψΈΣΗΚΘ§ΒΞΈΜΘΚ
ΈΣΉΦΘ§≥Τ÷ΊΦ« Ψ»γœ¬Θ®≥§ΙΐΈΣ’ΐΘ§≤ΜΉψΈΣΗΚΘ§ΒΞΈΜΘΚ![]() Θ©ΘΚ
Θ©ΘΚ![]() Θ§
Θ§![]() Θ§0Θ§0.3Θ§
Θ§0Θ§0.3Θ§ ![]() Θ§2.
Θ§2.
Θ®1Θ©Έ ’β6œδΤΜΙϊΒΡΉή÷ΊΝΩ «Εύ…ΌΘΩ
Θ®2Θ©‘Ύ≥ω έ’β≈ζΤΜΙϊ ±Θ§”–![]() ΒΡΤΜΙϊάΟΒτΘ®≤ΜΡή≥ω έΘ©Θ§»τ≥ω έΦέΈΣ8‘Σ/
ΒΡΤΜΙϊάΟΒτΘ®≤ΜΡή≥ω έΘ©Θ§»τ≥ω έΦέΈΣ8‘Σ/![]() Θ§¬τΆξ’β≈ζΤΜΙϊΗΟΥ°ΙϊΒξΩ…Ω…”°άϊΕύ…Ό‘ΣΘΩ
Θ§¬τΆξ’β≈ζΤΜΙϊΗΟΥ°ΙϊΒξΩ…Ω…”°άϊΕύ…Ό‘ΣΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90ΓψΘ§CDΓΆAB”ΎΒψDΘ§ΓœACD=3ΓœBCDΘ§E «–±±ΏABΒΡ÷–Βψ,‘ρΓœECDΒΡΕ» ΐΈΣ__________Ε».

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®1Θ©Α―œ¬Ν–Ης ΐΖ÷±πΧν‘Ύœύ”ΠΒΡΦ·ΚœάοΘΚ
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§0Θ§
Θ§0Θ§![]() Θ§Γ≠Γ≠
Θ§Γ≠Γ≠
’ΐ”–άμ ΐΦ·ΚœΘΚ{ Γ≠}
’ϊ ΐΦ·ΚœΘΚ{ Γ≠}
Ζ÷ ΐΦ·ΚœΘΚ{ Γ≠}
Θ®2Θ©‘Ύœ¬ΟφΒΡ ΐ÷α…œ±μ Ψœ¬Ν–Ης ΐΘ§≤ΔΑ¥’’¥”–ΓΒΫ¥σΒΡΥ≥–ρ”ΟΓΑ<Γ±Κ≈Ν§Ϋ”Τπά¥
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]()

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ![]() ΝΫΒΊœύΨύ
ΝΫΒΊœύΨύ![]() «ßΟΉΘ§ΦΉΓΔ““ΝΫ»ΥΕΦ¥”
«ßΟΉΘ§ΦΉΓΔ““ΝΫ»ΥΕΦ¥”![]() ΒΊ»Ξ
ΒΊ»Ξ![]() ΒΊΘ§ΆΦ÷–
ΒΊΘ§ΆΦ÷–![]() ΚΆ
ΚΆ![]() Ζ÷±π±μ ΨΦΉΓΔ““ΝΫ»ΥΥυΉΏ¬Ζ≥Χ
Ζ÷±π±μ ΨΦΉΓΔ““ΝΫ»ΥΥυΉΏ¬Ζ≥Χ![]() («ßΟΉ)”κ ±Φδ
(«ßΟΉ)”κ ±Φδ![]() (–Γ ±)÷°ΦδΒΡΙΊœΒΘ°Ε‘”Ύœ¬Ν–ΥΒΖ®ΘΚΔΌ““Άμ≥ωΖΔ
(–Γ ±)÷°ΦδΒΡΙΊœΒΘ°Ε‘”Ύœ¬Ν–ΥΒΖ®ΘΚΔΌ““Άμ≥ωΖΔ![]() –Γ ±ΘΜΔΎ““≥ωΖΔ
–Γ ±ΘΜΔΎ““≥ωΖΔ![]() –Γ ±ΚσΉΖ…œΦΉΘΜΔέΦΉΒΡΥΌΕ» «
–Γ ±ΚσΉΖ…œΦΉΘΜΔέΦΉΒΡΥΌΕ» «![]() «ßΟΉ/–Γ ±ΘΜΔή““œ»ΒΫ¥ο
«ßΟΉ/–Γ ±ΘΜΔή““œ»ΒΫ¥ο![]() ΒΊΘ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
ΒΊΘ§Τδ÷–’ΐ»ΖΒΡΗω ΐ «Θ® Θ©
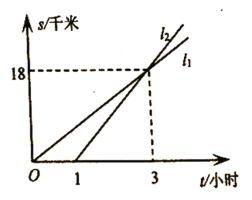
A.![]() ΗωB.3ΗωC.2ΗωD.1Ηω
ΗωB.3ΗωC.2ΗωD.1Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΙΪΥΨœζ έ≤ΩΟ≈ΧαΙ©ΝΥΡ≥÷÷≤ζΤΖœζ έ ’»κ(Φ«ΈΣ: ![]() /‘Σ)ΓΔœζ έ≥…±Ψ(Φ«ΈΣ:
/‘Σ)ΓΔœζ έ≥…±Ψ(Φ«ΈΣ:![]() /‘Σ)ΓΔœζ έΝΩ(Φ«ΈΣ:
/‘Σ)ΓΔœζ έΝΩ(Φ«ΈΣ: ![]() /Ε÷)ΖΫΟφΒΡ–≈œΔ»γœ¬:
/Ε÷)ΖΫΟφΒΡ–≈œΔ»γœ¬:
ΔΌ![]() ±Θ§
±Θ§![]() ;
;
ΔΎ![]() ±Θ§
±Θ§![]()
![]() ;
;
Δέ![]() ”κ
”κ![]() ≥…’ΐ±»άΐΚ· ΐΙΊœΒ;Δή
≥…’ΐ±»άΐΚ· ΐΙΊœΒ;Δή![]() ”κ
”κ![]() ≥…“Μ¥ΈΚ· ΐΙΊœΒΘ°
≥…“Μ¥ΈΚ· ΐΙΊœΒΘ°
“άΨί…œ ω–≈œΔΘ§ΫβΨωœ¬Ν–Έ Χβ:
Θ®1Θ©Ζ÷±π«σ≥ω![]() ”κ
”κ![]() ΒΡΚ· ΐΙΊœΒ Ϋ;
ΒΡΚ· ΐΙΊœΒ Ϋ;
Θ®2Θ©œζ έΝΩΈΣΕύ…ΌΕ÷ ±Θ§œζ έ ’»κ”κœζ έ≥…±ΨœύΆ§?
Θ®3Θ©»τœζ έΝΩΈΣ![]() Ε÷ ±Θ§«σΙΪΥΨΒΡάϊ»σΘ° (άϊ»σ=œζ έ ’»κ-œζ έ≥…±Ψ)
Ε÷ ±Θ§«σΙΪΥΨΒΡάϊ»σΘ° (άϊ»σ=œζ έ ’»κ-œζ έ≥…±Ψ)
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ[≤ΡΝœ‘ΡΕΝ]
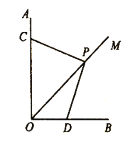
≤ΡΝœ“ΜΘΚ»γΆΦΘ§![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡΤΫΖ÷œΏ
ΒΡΤΫΖ÷œΏ![]() …œΘ§
…œΘ§![]() Θ§Βψ
Θ§Βψ![]() Θ§DΖ÷±π‘Ύ
Θ§DΖ÷±π‘Ύ![]() …œΘ°Ω…«σΒΟ»γœ¬Ϋα¬έΘΚ
…œΘ°Ω…«σΒΟ»γœ¬Ϋα¬έΘΚ![]() Θ§
Θ§![]() ΈΣΕ®÷ΒΘ°
ΈΣΕ®÷ΒΘ°
≤ΡΝœΕΰ(–‘÷ )ΘΚΥΡ±Ώ–ΈΒΡΡΎΫ«ΚΆΈΣ![]() Θ°
Θ°
[Έ ΧβΫβΨω]
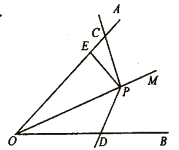
Θ®1Θ©»γΆΦΘ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡΤΫΖ÷œΏ
ΒΡΤΫΖ÷œΏ![]() …œΘ§
…œΘ§![]() ΒΡ±Ώ”κ
ΒΡ±Ώ”κ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§«“
Θ§«“![]() Θ§«σ
Θ§«σ![]() ΒΡ÷Β(”ΟΚ§
ΒΡ÷Β(”ΟΚ§![]() ΒΡ ΫΉ”±μ Ψ)Θ°
ΒΡ ΫΉ”±μ Ψ)Θ°
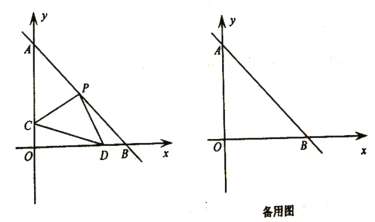
Θ®2Θ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§÷±œΏ![]() ”κ
”κ![]() ÷αΘ§
÷αΘ§![]() ÷αΖ÷±πΫΜ”Ύ
÷αΖ÷±πΫΜ”Ύ![]() ΝΫΒψΘ§Βψ
ΝΫΒψΘ§Βψ![]() «
«![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§![]() Θ§
Θ§![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() ,
,![]() ”κ
”κ![]() ÷αΒΡ’ΐΑκ÷αΫΜ”ΎΒψ
÷αΒΡ’ΐΑκ÷αΫΜ”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ°«σ
Θ°«σ![]() ΒΡ≥ΛΕ»Θ°
ΒΡ≥ΛΕ»Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘ§»γΆΦΘ§‘ΎΤ¬ΕΞA¥ΠΒΡΆ§“ΜΥ°ΤΫΟφ…œ”–“ΜΉυΙ≈ΥΰBCΘ§ ΐ―ß–Υ»Λ–ΓΉιΒΡΆ§―ß‘Ύ–±Τ¬ΒΉP¥Π≤βΒΟΗΟΥΰΒΡΥΰΕΞBΒΡ―ωΫ«ΈΣ45ΓψΘ§»ΜΚσΥϊΟ«―ΊΉ≈Τ¬Ε»ΈΣ1ΘΚ2.4ΒΡ–±Τ¬AP≈ ––ΝΥ26ΟΉΘ§‘ΎΤ¬ΕΞA¥Π”÷≤βΒΟΗΟΥΰΒΡΥΰΕΞBΒΡ―ωΫ«ΈΣ76ΓψΘ°
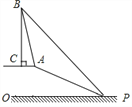
«σΘΚΘ®1Θ©Τ¬ΕΞAΒΫΒΊΟφPOΒΡΨύάκΘΜ
Θ®2Θ©Ι≈ΥΰBCΒΡΗΏΕ»Θ®ΫαΙϊΨΪ»ΖΒΫ1ΟΉΘ©Θ°
Θ®≤ΈΩΦ ΐΨίΘΚsin76ΓψΓ÷0.97Θ§cos76ΓψΓ÷0.24Θ§tan76ΓψΓ÷4.01Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―ß–ΘΈΣ ΙΗΏ“Μ–¬…ζ»κ–ΘΚσΦΑ ±¥©…œΚœ…μΒΡ–ΘΖΰΘ§œ÷Χα«ΑΕ‘Ρ≥–ΘΨ≈ΡξΦΕ»ΐΑύ―ß…ζΦ¥ΫΪΥυ¥©–ΘΖΰ–ΆΚ≈«ιΩωΫχ––ΝΥΟΰΒΉΒς≤ιΘ§≤ΔΗυΨίΒς≤ιΫαΙϊΜφ÷ΤΝΥ»γΆΦΝΫΗω≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘ®–ΘΖΰ–ΆΚ≈“‘…μΗΏΉςΈΣ±ξΉΦΘ§Ι≤Ζ÷ΈΣ6Ηω–ΆΚ≈Θ©
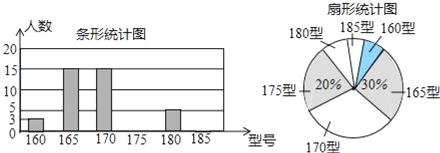
ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©ΗΟΑύΙ≤”–ΓΓΓΓΟϊ―ß…ζΘΜ
Θ®2Θ©‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§185–Ά–ΘΖΰΥυΕ‘”ΠΒΡ…»–Έ‘≤–ΡΫ«ΒΡ¥σ–ΓΈΣΓΓΓΓΘΜ
Θ®3Θ©ΗΟΑύ―ß…ζΥυ¥©–ΘΖΰ–ΆΚ≈ΒΡ÷Ύ ΐΈΣΓΓΓΓΓΓΘ§÷–ΈΜ ΐΈΣΓΓΓΓΘΜ
Θ®4Θ©»γΙϊΗΟ–Θ‘ΛΦΤ’– ’–¬…ζ600ΟϊΘ§ΗυΨί―υ±Ψ ΐΨίΘ§ΙάΦΤ–¬…楩170–Ά–ΘΖΰΒΡ―ß…ζ¥σ‘Φ”–Εύ…ΌΟϊΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com