
【题目】如图,平面直角坐标系中,已知A(2,2)、B(4,0),若在x轴上取点C,使△ABC为等腰三角形,则满足条件的点C的个数是( )
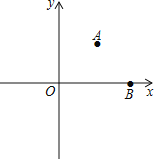
A. 1B. 2C. 3D. 4
【答案】D
【解析】
由点A、B的坐标可得到AB=2![]() ,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.
,然后分类讨论:若AC=AB;若BC=AB;若CA=CB,确定C点的个数.
∵点A、B的坐标分别为(2,2)、B(4,0).
∴AB=2![]() ,
,
如图,①若AC=AB,以A为圆心,AB为半径画弧与x轴有2个交点(含B点),即(0,0)、(4,0),
∴满足△ABC是等腰三角形的C点有1个;
②若BC=AB,以B为圆心,BA为半径画弧与x轴有2个交点,即满足△ABC是等腰三角形的C点有2个;
③若CA=CB,作AB的垂直平分线与x轴有1个交点,即满足△ABC是等腰三角形的C点有1个;
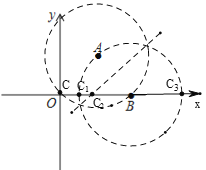
综上所述:点C在x轴上,△ABC是等腰三角形,符合条件的点C共有4个.
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将连续的正偶数2,4,6,8…,排成下表:
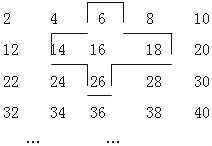
(1)十字框中的五个数的和是中间的数16的几倍?
(2)若将十字框上下左右移动,可框住另外的五个数,设中间的数为![]() ,用代数式表示十字框中的五个数的和;
,用代数式表示十字框中的五个数的和;
(3)这五个数的和能等于2010吗?如能,写出这五个数,如不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材母题 点P(x,y)在第一象限,且x+y=8,点A的坐标为(6,0).设△OPA的面积为S.
(1)用含有x的式子表示S,写出x的取值范围,画出函数S的图象;
(2)当点P的横坐标为5时,△OPA的面积为多少?
(3)△OPA的面积能大于24吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
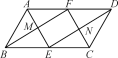
【题目】如图,ABCD中,∠ABC=60°,AB=4,AD=8,点E,F分别是边BC,AD的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
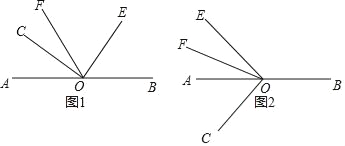
【题目】已知点O是AB上的一点,∠COE=90°,OF平分∠AOE.
(1)如图1,当点C,E,F在直线AB的同一侧时,若∠AOC=40°,求∠BOE和∠COF的度数;
(2)在(1)的条件下,∠BOE和∠COF有什么数量关系?请直接写出结论,不必说明理由;
(3)如图2,当点C,E,F分别在直线AB的两侧时,若∠AOC=β,那么(2)中∠BOE和∠COF的数量关系是否仍然成立?请写出结论,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于点D,BD=3cm,DC=8cm,AD=4cm,动点P从点B出发,沿折线BA﹣AC向终点C做匀速运动,点P在线段BA上的运动速度是5cm/s;在线段AC上的运动速度是![]() cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
cm/s,当点P不与点B、C重合时,过点P作PQ⊥BC于点Q,将△PBQ绕PQ的中点旋转180°得到△QB′P,设四边形PBQB′与△ABD重叠部分图形的面积为y(cm2),点P的运动时间为x(s).
(1)用含x的代数式表示线段AP的长.
(2)当点P在线段BA上运动时,求y与x之间的函数关系式.
(3)当经过点B′和△ADC一个顶点的直线平分△ADC的面积时,直接写出x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
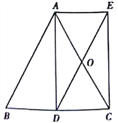
【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com