
ЁОЬтФПЁПвбжЊЕуOЪЧABЩЯЕФвЛЕуЃЌЁЯCOEЃН90ЁуЃЌOFЦНЗжЁЯAOEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуCЃЌEЃЌFдкжБЯпABЕФЭЌвЛВрЪБЃЌШєЁЯAOCЃН40ЁуЃЌЧѓЁЯBOEКЭЁЯCOFЕФЖШЪ§ЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЁЯBOEКЭЁЯCOFгаЪВУДЪ§СПЙиЯЕЃПЧыжБНгаДГіНсТлЃЌВЛБиЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБЕуCЃЌEЃЌFЗжБ№дкжБЯпABЕФСНВрЪБЃЌШєЁЯAOCЃНІТЃЌФЧУДЃЈ2ЃЉжаЁЯBOEКЭЁЯCOFЕФЪ§СПЙиЯЕЪЧЗёШдШЛГЩСЂЃПЧыаДГіНсТлЃЌВЂЫЕУїРэгЩЃЎ
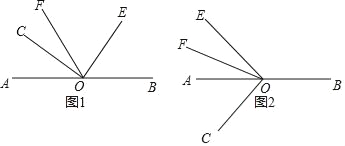
ЁОД№АИЁП(1) ЁЯCOFЃН25Ёу, ЁЯBOEЃН50ЁуЃЛ(2) ЁЯBOEЃН2ЁЯCOF;(3) ЁЯBOEЃН2ЁЯCOF,РэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓГіЁЯBOEКЭЁЯCOFЕФЖШЪ§МДПЩХаЖЯЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉМДПЩЧѓНтЃЛ
ЃЈ3ЃЉНсТлЃКЁЯBOEЃН2ЁЯCOFЃЎИљОнНЧЕФКЭВюЖЈвхМДПЩНтОіЮЪЬтЃЎ
НтЃКЃЈ1ЃЉЁпЁЯCOEЃН90ЁуЃЌЁЯAOCЃН40ЁуЃЌ
ЁрЁЯBOEЃН180ЁуЉЁЯAOCЉЁЯCOEЃН180ЁуЉ40ЁуЉ90ЁуЃН50ЁуЃЌ
ЁЯAOEЃНЁЯAOC+ЁЯCOEЃН40Ёу+90ЁуЃН130ЁуЃЌ
ЁпOFЦНЗжЁЯAOEЃЌ
ЁрЁЯEOFЃН![]() ЁЯAOEЃН
ЁЯAOEЃН![]() ЁС130ЁуЃН65ЁуЃЌ
ЁС130ЁуЃН65ЁуЃЌ
ЁрЁЯCOFЃНЁЯCOEЉЁЯEOFЃН90ЁуЉ65ЁуЃН25ЁуЃЛ
ЃЈ2ЃЉЁЯBOEЃН2ЁЯCOFЃЎ
ЃЈ3ЃЉЁЯBOEЃН2ЁЯCOFЃЎ
РэгЩШчЯТЃКЁпЁЯCOEЃН90ЁуЃЌЁЯAOCЃНІТЃЌ
ЁрЁЯAOEЃНЁЯCOEЉЁЯAOCЃН90ЁуЉІТЃЌ
ЁрЁЯBOEЃН180ЁуЉЁЯAOEЃН180ЁуЉЃЈ90ЁуЉІТЃЉЃН90Ёу+ІТЃЌ
ЁпOFЦНЗжЁЯAOEЃЌ
ЁрЁЯAOFЃН![]() ЁЯAOEЃН
ЁЯAOEЃН![]() ЃЈ90ЁуЉІТЃЉЃН45ЁуЉ
ЃЈ90ЁуЉІТЃЉЃН45ЁуЉ![]() ІТЃЌ
ІТЃЌ
ЁрЁЯCOFЃНІТ+ЃЈ45ЁуЉ![]() ІТЃЉЃН45Ёу+
ІТЃЉЃН45Ёу+![]() ІТЃЌ
ІТЃЌ
Ёр2ЁЯCOFЃН2ЃЈ45Ёу+![]() ІТЃЉЃН90Ёу+ІТЃЌ
ІТЃЉЃН90Ёу+ІТЃЌ
ЁрЁЯBOEЃН2ЁЯCOFЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЕу![]() ЮЊе§ЗНаЮ
ЮЊе§ЗНаЮ![]() ЕФжааФЁЃ
ЕФжааФЁЃ
ЃЈ1ЃЉНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыЗНЯђа§зЊ
ФцЪБеыЗНЯђа§зЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФЖдгІЕуЮЊЕу
ЕФЖдгІЕуЮЊЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЧывРЬтвтВЙШЋЭМ1ЃЛ
ЃЌЧывРЬтвтВЙШЋЭМ1ЃЛ
ЃЈ2ЃЉИљОнЭМ1жаВЙШЋЕФЭМаЮЃЌВТЯыВЂжЄУї![]() гы
гы![]() ЕФЙиЯЕЃЛ
ЕФЙиЯЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕу![]() ЪЧ
ЪЧ![]() жаЕуЃЌЁї
жаЕуЃЌЁї![]() ЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЪЧЕШбќжБНЧШ§НЧаЮЃЌ ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЁї
ЃЌЁї![]() ШЦ
ШЦ![]() ЕуФцЪБеыЗНЯђа§зЊ
ЕуФцЪБеыЗНЯђа§зЊ![]() НЧЖШЃЌЧыжБНгаДГіа§зЊЙ§ГЬжа
НЧЖШЃЌЧыжБНгаДГіа§зЊЙ§ГЬжа![]() ЕФзюДѓжЕЁЃ
ЕФзюДѓжЕЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАгжЬ№гжДрЁБЫЎЙћЕъЯжДгХњЗЂЪаГЁТђНј6ЯфЦЛЙћЃЌТђНјМлУПЯф40дЊЃЌвдУПЯф![]() ЮЊзМЃЌГЦжиМЧЪОШчЯТЃЈГЌЙ§ЮЊе§ЃЌВЛзуЮЊИКЃЌЕЅЮЛЃК
ЮЊзМЃЌГЦжиМЧЪОШчЯТЃЈГЌЙ§ЮЊе§ЃЌВЛзуЮЊИКЃЌЕЅЮЛЃК![]() ЃЉЃК
ЃЉЃК![]() ЃЌ
ЃЌ![]() ЃЌ0ЃЌ0.3ЃЌ
ЃЌ0ЃЌ0.3ЃЌ ![]() ЃЌ2.
ЃЌ2.
ЃЈ1ЃЉЮЪет6ЯфЦЛЙћЕФзмжиСПЪЧЖрЩйЃП
ЃЈ2ЃЉдкГіЪлетХњЦЛЙћЪБЃЌга![]() ЕФЦЛЙћРУЕєЃЈВЛФмГіЪлЃЉЃЌШєГіЪлМлЮЊ8дЊ/
ЕФЦЛЙћРУЕєЃЈВЛФмГіЪлЃЉЃЌШєГіЪлМлЮЊ8дЊ/![]() ЃЌТєЭъетХњЦЛЙћИУЫЎЙћЕъПЩПЩгЎРћЖрЩйдЊЃП
ЃЌТєЭъетХњЦЛЙћИУЫЎЙћЕъПЩПЩгЎРћЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
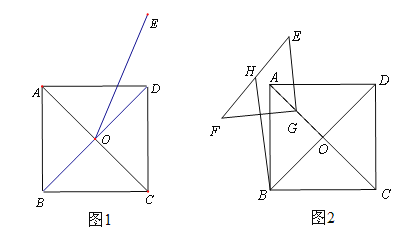
ЁОЬтФПЁПШчЭМЃЌдкЁѕABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌABЁЭACЃЌABЃН3cmЃЌBCЃН5cm.ЕуPДгAЕуГіЗЂбиADЗНЯђдШЫйдЫЖЏЃЌЫйЖШЮЊ1cm/s.СЌНсPOВЂбгГЄНЛBCгкЕуQЃЌЩшдЫЖЏЪБМфЮЊt(0ЃМtЃМ5)ЃЎ
(1)ЕБtЮЊКЮжЕЪБЃЌЫФБпаЮABQPЪЧЦНааЫФБпаЮЃП
(2)ЩшЫФБпаЮOQCDЕФУцЛ§ЮЊy(cm2)ЃЌЧѓyгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕуOдкЯпЖЮAPЕФДЙжБЦНЗжЯпЩЯЃПШєДцдкЃЌЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
 ЁЁЁЁ
ЁЁЁЁ БИгУЭМ
БИгУЭМ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌвбжЊA(2ЃЌ2)ЁЂB(4ЃЌ0)ЃЌШєдкxжсЩЯШЁЕуCЃЌЪЙЁїABCЮЊЕШбќШ§НЧаЮЃЌдђТњзуЬѕМўЕФЕуCЕФИіЪ§ЪЧ( )
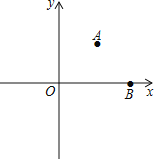
A. 1B. 2C. 3D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
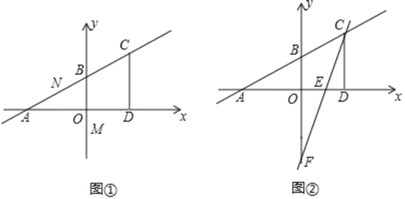
ЁОЬтФПЁПШчЭМЃЌжБЯпABЃКyЃН![]() x+2гыxжсЁЂyжсЗжБ№НЛгкAЃЌBСНЕуЃЌCЪЧЕквЛЯѓЯоФкжБЯпABЩЯвЛЕуЃЌЙ§ЕуCзїCDЁЭxжсгкЕуDЃЌЧвCDЕФГЄЮЊ
x+2гыxжсЁЂyжсЗжБ№НЛгкAЃЌBСНЕуЃЌCЪЧЕквЛЯѓЯоФкжБЯпABЩЯвЛЕуЃЌЙ§ЕуCзїCDЁЭxжсгкЕуDЃЌЧвCDЕФГЄЮЊ![]() ЃЌPЪЧxжсЩЯЕФЖЏЕуЃЌNЪЧжБЯпABЩЯЕФЖЏЕуЃЎ
ЃЌPЪЧxжсЩЯЕФЖЏЕуЃЌNЪЧжБЯпABЩЯЕФЖЏЕуЃЎ
ЃЈ1ЃЉжБНгаДГіAЃЌBСНЕуЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМЂйЃЌШєЕуMЕФзјБъЮЊЃЈ0ЃЌ![]() ЃЉЃЌЪЧЗёДцдкетбљЕФPЕуЃЎЪЙвдOЃЌPЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєгадкЃЌЧыЧѓГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЉЃЌЪЧЗёДцдкетбљЕФPЕуЃЎЪЙвдOЃЌPЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃПШєгадкЃЌЧыЧѓГіPЕузјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМЂкЃЌНЋжБЯпABШЦЕуCФцЪБеыа§зЊНЛyжсгкЕуFЃЌНЛxжсгкЕуEЃЌШєа§зЊНЧМДЁЯACEЃН45ЁуЃЌЧѓЁїBFCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌCDЁЭABгкЕуDЃЌЁЯACD=3ЁЯBCDЃЌEЪЧаББпABЕФжаЕу,дђЁЯECDЕФЖШЪ§ЮЊ__________ЖШ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉАбЯТСаИїЪ§ЗжБ№ЬюдкЯргІЕФМЏКЯРяЃК
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ0ЃЌ
ЃЌ0ЃЌ![]() ЃЌЁЁ
ЃЌЁЁ
е§гаРэЪ§МЏКЯЃК{ Ё}
ећЪ§МЏКЯЃК{ Ё}
ЗжЪ§МЏКЯЃК{ Ё}
ЃЈ2ЃЉдкЯТУцЕФЪ§жсЩЯБэЪОЯТСаИїЪ§ЃЌВЂАДееДгаЁЕНДѓЕФЫГађгУЁА<ЁБКХСЌНгЦ№РД
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌдкЦТЖЅAДІЕФЭЌвЛЫЎЦНУцЩЯгавЛзљЙХЫўBCЃЌЪ§бЇаЫШЄаЁзщЕФЭЌбЇдкаБЦТЕзPДІВтЕУИУЫўЕФЫўЖЅBЕФбіНЧЮЊ45ЁуЃЌШЛКѓЫћУЧбизХЦТЖШЮЊ1ЃК2.4ЕФаБЦТAPХЪааСЫ26УзЃЌдкЦТЖЅAДІгжВтЕУИУЫўЕФЫўЖЅBЕФбіНЧЮЊ76ЁуЃЎ
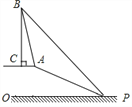
ЧѓЃКЃЈ1ЃЉЦТЖЅAЕНЕиУцPOЕФОрРыЃЛ
ЃЈ2ЃЉЙХЫўBCЕФИпЖШЃЈНсЙћОЋШЗЕН1УзЃЉЃЎ
ЃЈВЮПМЪ§ОнЃКsin76ЁуЁж0.97ЃЌcos76ЁуЁж0.24ЃЌtan76ЁуЁж4.01ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com