
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,BE平分∠ABC交AD于F,交AC于E,若EG⊥BC于G,连结FG.说明四边形AFGE是菱形.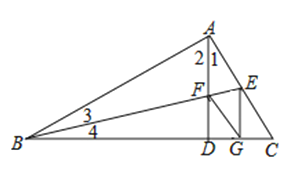
【答案】证明:∵在Rt△ABC中,∠BAC=90°,
∴BA⊥AE,
∵BE平分∠ABC,EG⊥BC,
∴∠3=∠4,AE=EG,
∵AD⊥BC,
∴AD∥EG,∠AFE=∠BFD=90°﹣∠4,
∵∠AEF=90°﹣∠3,
∴∠AEF=∠AFE,
∴AF=AE,
∴AF=EG,
∴四边形AFGE是平行四边形,
∴AFGE是菱形.
【解析】由在Rt△ABC中,∠BAC=90°,EG⊥BC,BE平分∠ABC,根据角平分线的性质,可得AE=EG,易求得△AEF是等腰三角形,即可得AF=AE=EG,继而证得四边形AFGE是平行四边形,则可得四边形AFGE是菱形.
【考点精析】根据题目的已知条件,利用菱形的判定方法的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】天安门广场的面积约440000平方米. 440000这个数用科学计数法表示为
A. 44×104. B. 4.4×105. C. 0.44×106. D. 4.4×104.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中,不能确定四边形ABCD为平行四边形的是( )
A. ∠A=∠C,∠B=∠D B. ∠A=∠B=∠C=90°
C. ∠A+∠B=180°,∠B+∠C=180° D. ∠A+∠B=180°,∠C+∠D=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)求证:△CBG≌△CDG;
(2)求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;
(3)连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.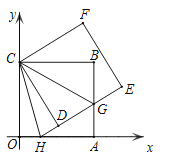
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△AˊBˊCˊ关于点O对称,下列结论不正确的是( )
A. AO=AˊO
B. AB∥AˊBˊ
C. CO=BO
D. ∠BAC=∠BˊAˊCˊ
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,过点D作DE⊥AB于点E,点F 在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求证:AF平分∠DAB.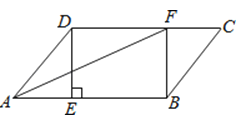
查看答案和解析>>
科目:初中数学 来源: 题型:
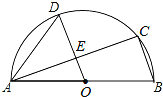
【题目】如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=72°,求∠CAD的度数;
(2)若AB=13,AC=12,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com