(1)证明:∵AE⊥BD,
∴弧BE=弧DE.
∴∠1=∠2.
∵∠3=∠4,∠5=∠2+∠3,∠IBE=∠1+∠4,
∴∠5=∠IBE.

∴BE=IE.
(2)解:连接QC、TB,
则∠6+∠CBQ=90°,
又∠7+∠8=90°,而∠6=∠7,
∴∠CBQ=∠8=∠9.
∴△ABG∽△ATB.
∴AB
2=AG•AT.
∵AI⊥CE,
∴I为CE的中点.
∴AE=AC,IE=IC.
∴△BEO∽△CBE.
∴OE:OB=BE:CE=1:2.
设⊙A的半径为R,
由AB
2-OA
2=BO
2,OE=R-3,
得R
2-3
2=4(R-3)
2解得R=5,或R=3(不合题意,舍去).
∴AT•AG=AB
2=25.
(方法二提示:可连接AD、CD证△BAG∽△TAD)
(3)解:②的值不变.

证明:作O
1K⊥MN于K,连接O
1N、PN、BM,
则MN=2NK,且∠N O
1K=∠1,
∴
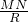
=

=2sin∠NO
1K=2sin∠1
由直线y=x+3得OB=OD=4,OM⊥BD,
∴∠2=∠3.
又∠2=∠4+∠5,∠3=∠2+∠6,
∵∠5=∠6,
∴∠1=∠4=∠NO
1K,=2sin∠4=2×

=

.
所以
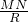
的值不变,其值为

.
分析:(1)已知AE⊥BD,由垂径定理得,弧BE=弧DE,由圆周角定理得∠1=∠2,AH是∠ABO的平分线,则∠3=∠4,由三角形的外角等于与它不相邻的两个内角和得,∠5=∠2+∠3,∠IBE=∠1+∠4,所以∠5=∠IBE,由等角对等边得证BE=IE;
(2)连接QC、TB,由同角或等角的余角相等得,∠CBQ=∠8=∠9,可证△ABG∽△ATB得到AB
2=AG•AT,又因为AH⊥CE,由垂径定理得,H为CE的中点,即BE=EC,得证△BEO∽△CBE,得OE:OB=BE:CE=1:2,设⊙A的半径为R,由勾股定理得,AB
2-OA
2=BO
2,OE=R-3,可求得,R=5,即AT•AG=AB
2=25;(方法二提示:可连接AD、CD证△BAG∽△TAD)
(3)②的值不变.作O
1K⊥MN于K,连接O
1N、PN、BM,由垂径定理得,MN=2NK,且∠N O
1K=∠1,由正弦的概念得,
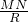
=

=2sin∠NO
1K=2sin∠1,由直线y=x+3求得OB=OD=4,即OM⊥BD,由垂径定理得∠2=∠3,由三角形的外角与内角的关系得:∠2=∠4+∠5,∠3=∠2+∠6,由圆周角定理知∠5=∠6,所以∠1=∠4=∠NO
1K,=2sin∠4=2×

=

.
点评:本题利用了垂径定理,直角三角形的性质,全等三角形和相似三角形的判定及性质,勾股定理圆周角定理,一次函数的图象与坐标轴的关系,三角形的外角与内角的关系求解,综合性强,涉及多个知识点.

 时,给出下列两个结论:①MN的长度不变;②
时,给出下列两个结论:①MN的长度不变;②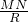 的值不变,其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.
的值不变,其中有且只有一个结论是正确的,请你判断哪一个结论正确,证明正确的结论并求出其值.



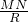 =
= =2sin∠NO1K=2sin∠1
=2sin∠NO1K=2sin∠1 =
= .
.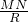 的值不变,其值为
的值不变,其值为 .
.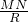 =
= =2sin∠NO1K=2sin∠1,由直线y=x+3求得OB=OD=4,即OM⊥BD,由垂径定理得∠2=∠3,由三角形的外角与内角的关系得:∠2=∠4+∠5,∠3=∠2+∠6,由圆周角定理知∠5=∠6,所以∠1=∠4=∠NO1K,=2sin∠4=2×
=2sin∠NO1K=2sin∠1,由直线y=x+3求得OB=OD=4,即OM⊥BD,由垂径定理得∠2=∠3,由三角形的外角与内角的关系得:∠2=∠4+∠5,∠3=∠2+∠6,由圆周角定理知∠5=∠6,所以∠1=∠4=∠NO1K,=2sin∠4=2× =
= .
.

 寒假学与练系列答案
寒假学与练系列答案 原点O及A、B两点.
原点O及A、B两点. 交于点G,垂足分别是E、F,AC是⊙O的弦,
交于点G,垂足分别是E、F,AC是⊙O的弦, 已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=
已知:如图,直线y=kx+b与x轴交于点A,且与双曲线y=