
【题目】一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
【答案】
(1)证明:CD与FG交于点M,
∵∠OCD=25°,四边形ABCD是矩形,∠FGB=65°.
∴∠FMC=65°,
∴∠MFC=90°,
∴GF⊥CO
(2)解:作GN⊥EH于点N,

∵FG∥EH,GF⊥CO;
∴四边形ENGF是矩形;
∴EF=NG,
∵∠FGB=∠NHG=65°,
∴sin65°= ![]() =
= ![]() ≈0.91,
≈0.91,
∴EF=NG=2.366m≈2.4m.
【解析】(1)利用矩形的性质和已知易证;
(2)作GN⊥EH于点N,易证四边形ENGF是矩形,可得EF=NG,在Rt△HGN中利用三角函数可求得NG,即可得到答案.
【考点精析】本题主要考查了平行线的性质和等腰三角形的性质的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=45°,AB=4cm.点P从点A出发,以2cm/s的速度沿边AB向终点B运动.过点P作PQ⊥AB交折线ACB于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).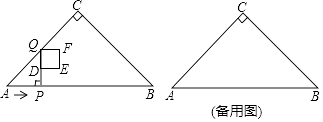
(1)当点Q在边AC上时,正方形DEFQ的边长为cm(用含x的代数式表示);
(2)当点P不与点B重合时,求点F落在边BC上时x的值;
(3)当0<x<2时,求y关于x的函数解析式;
(4)直接写出边BC的中点落在正方形DEFQ内部时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(b,-2a).且![]() +|b-l|=0.CD∥AB,AD∥BC
+|b-l|=0.CD∥AB,AD∥BC
(1)直接写出B、C、D各点的坐标:B 、C 、D ;
(2)如图1,P(3,10),点E,M在四边形ABCD的边上,且E在第二象限.若△PEM是以PE为直角边的等腰直角三角形,请直接写出点E的坐标,并对其中一种情况计算说明;
(3)如图2,F为y轴正半轴上一动点,过F的直线j∥x轴,BH平分∠FBA交直线j于点H.G为BF上的点,且∠HGF=∠FAB,F在运动中FG的长度是否发生变化?若变化,求出变化范围;若不变,求出定值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2x、宽为2y的长方形,沿图中虚线用剪刀剪成四个完全相同的小长方形,然后按图2所示拼成一个正方形.
(1)你认为图2中的阴影部分的正方形的边长等于
(2)试用两种不同的方法求图2中阴影部分的面积.
方法1: 方法2:
(3)根据图2你能写出下列三个代数式之间的等量关系吗?
代数式:(x+y)2,(x-y)2,4xy.
(4)根据(3)题中的等量关系,解决如下问题:
若x+y=4,xy=3,则(x-y)2=
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB,∠A=50°,P是△ABC内一点,且∠ACP=∠PBC,则∠BPC的度数为( )

A. 130° B. 115° C. 110° D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若点C在线段AB的延长线上,且满足AC-BC=b,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形并写出你的结论(不必说明理由).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点 A(a+b,2-a)与点B(a-5,b-2a)关于y轴对称.
(1)求A、B两点的坐标;
(2)如果点B关于x轴的对称点是C,在图中标出点A、B、C,并求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
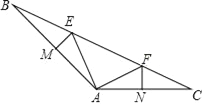
【题目】如图,已知△ABC中∠BAC=135°,点E,点F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,BE=12,CF=9.
(1)判断△EAF的形状,并说明理由;
(2)求△EAF的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com