
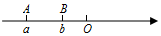
 已知a、b表示两个不同点A、B的有理数,且|a|=5,|b|=2,它们在数轴的位置如图所示.
已知a、b表示两个不同点A、B的有理数,且|a|=5,|b|=2,它们在数轴的位置如图所示.分析 (1)根据绝对值的定义结合由数轴得出a、b的符号即可得;
(2)根据数轴上两点间的距离公式即可得;
(3)设C点表示的数为x,分以下两种情况:点C在A、B之间、点C在点B右侧,利用两点间距离公式列方程求解.
解答 解:(1)∵|a|=5,|b|=2,
∴a=5或-5,b=2或-2,
由数轴可知,a<b<0,
∴a=-5,b=-2;
(2)表示a、b两数的点之间的距离为-2-(-5)=3;
(3)设C点表示的数为x,
当点C在A、B之间时,根据题意有:x-(-5)=3(-2-x),
解得:x=-$\frac{11}{4}$;
当点C在点B右侧时,根据题意有:x-(-5)=3[x-(-2)],
解得:x=-$\frac{1}{2}$;
∴C点表示的数为-$\frac{1}{2}$或-$\frac{11}{4}$.
点评 本题主要考查绝对值和数轴及两点间的距离公式,根据题意分类讨论思想的运用是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
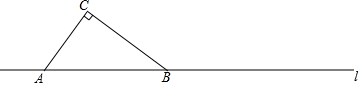
 铁路上A,B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,请画出E点位置(要求尺规作图,保留作图痕迹)并求出E站应建在离A站多少千米处?
铁路上A,B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,请画出E点位置(要求尺规作图,保留作图痕迹)并求出E站应建在离A站多少千米处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com