
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
解答 解:①52+122=132,能构成直角三角形;
②72+242=252,能构成直角三角形,能构成直角三角形;
③(3a)2+(4a)2=(5a)2,能构成直角三角形;
④(32)2+(42)2≠(52)2,不能构成直角三角形;
⑤($\sqrt{3}$)2+($\sqrt{4}$)2≠($\sqrt{5}$)2,不能构成直角三角形.
故可以构成直角三角形的边长有3组.
故选C.
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
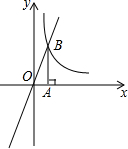 如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.
如图,正比例函数y=3x的图象与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点B.若k取1,2,3,…,10,对应的Rt△AOB的面积分别为S1,S2,…,S10,则S1+S2+…S10=$\frac{55}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com