
 如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为( )
如图,矩形ABCD绕点B逆时针旋转30°后得到矩形A1BC1D1,C1D1与AD交于点M,延长DA交A1D1于F,若AB=1,BC=$\sqrt{3}$,则AF的长度为( )| A. | 2-$\sqrt{3}$ | B. | $\frac{\sqrt{3}-1}{3}$ | C. | $\frac{3-\sqrt{3}}{3}$ | D. | $\sqrt{3}$-1 |
分析 方法1,先求出∠CBD,根据旋转角,判断出点C1在矩形对角线BD上,求出BD,再求出∠DBF,从而判断出DF=BD,即可.
方法2,延长BA交A1D1于H,先确定出∠AFD1=30°,在用含30°的直角三角形的性质依次求出BH,AF即可.
解答 解法1,:连接BD,如图所示: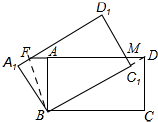
在矩形ABCD中,∠C=90°,CD=AB=1,
在Rt△BCD中,CD=1,BC=$\sqrt{3}$,
∴tan∠CBD=$\frac{CD}{BC}=\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,BD=2,
∴∠CBD=30°,∠ABD=60°,
由旋转得,∠CBC1=∠ABA1=30°,
∴点C1在BD上,
连接BF,
由旋转得,AB=A1B,
∵矩形A1BC1D1是矩形ABCD旋转所得,
∴∠BA1F=∠BAF=90°,
∵BF=BF,
∴△A1BF≌△ABF,
∴∠A1BF=∠ABF,
∵∠ABA1=30°,
∴∠ABF=$\frac{1}{2}$∠ABA1=15°,
∵∠ABD=60°,
∴∠DBF=75°,
∵AD∥BC,
∴∠ADB=∠CBD=30°,
∴∠BFD=75°,
∴DF=BD=2,
∴AF=DF-AD=2-$\sqrt{3}$,
方法2,如图,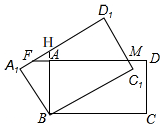 延长BA交A1D1于H,
延长BA交A1D1于H,
由旋转得,A1B=AB=1,∠CBC1=∠ABA1=30°,∠BA1D1=∠BAF=90°,
在四边形A1BAF中,根据四边形的内角和得,∠A1FA=150°,
∴∠AFH∠=30°,
在Rt△A1BH中,A1B=1,∠A1BA=30°,
∴BH=$\frac{2\sqrt{3}}{3}$,
∴AH=BH-AB=$\frac{2\sqrt{3}}{3}$-1
在Rt△AFH中,∠AFH=30°,
∴AF=$\sqrt{3}$AH=2-$\sqrt{3}$
故选:A.
点评 本题考查了旋转的性质、矩形的性质、全等三角形的判定与性质、等腰三角形的判定、三角函数;熟练掌握旋转的性质和矩形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线与y轴交于点C(0,3),与x轴交于点A、B,点A在点B的左边,且B(3,0),AB=2
如图,已知抛物线与y轴交于点C(0,3),与x轴交于点A、B,点A在点B的左边,且B(3,0),AB=2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查市场上酸奶的质量情况 | |
| B. | 调查某品牌圆珠笔芯的使用寿命 | |
| C. | 调查一架“歼20”战机各零部件的质量 | |
| D. | 调查我市市民对巴西奥运会吉祥物的知晓率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com