
���� ��1�����������߶���ĺ�����Ϊ1�ɵó������ߵĶԳ���Ϊx=1�����һ�����������Ϊ��4��0�������ɵó���һ����B�����꣬�ٸ��������ε������ʽ�������OC�ij��ȣ���������߿������ϣ����ɵó���C�����ꣻ
��2���ɵ�A��B��C��������꣬���ô���ϵ����������������ߵĽ���ʽ��
��3�������ô���ϵ�������ֱ��AC��BC�Ľ���ʽ����������������M�����꣬�ɴ˼��ɵó���N�����꣬�ٷ֡�OMN=90�㡢��PNM=90���Լ���MPN=90������������ǣ�ÿ������¸��ݵ���ֱ�������ε������ҳ�����m��һԪһ�η��̣��ⷽ�̼��ɵó���P�����꣮
��� �⣺��1���������⻭��ͼ�Σ���ͼ1��ʾ��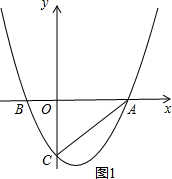
�߸������߶���ĺ�����Ϊ1��
�������ߵĶԳ���Ϊx=1��
��������y=ax2+bx+c��x���һ��������A��4��0����
����һ����B��-2��0����
��S��AOC=$\frac{1}{2}$OA•OC=$\frac{1}{2}$��4��OC=6��
��OC=3��
���C��������0��-3����
��2������A��4��0����B��-2��0����C��0��-3������y=ax2+bx+c��
�ã�$\left\{\begin{array}{l}{16a+4b+c=0}\\{4a-2b+c=0}\\{c=-3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=\frac{3}{8}}\\{b=-\frac{3}{4}}\\{c=-3}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{3}{8}{x}^{2}$-$\frac{3}{4}$x-3��
��3����A��4��0����B��-2��0����C��0��-3����
��ֱ��AC�Ľ���ʽΪy=k1x-3��ֱ��BC�Ľ���ʽΪy=k2x-3��
��0=4k1-3��-2k2-3=0��
��ã�k1=$\frac{3}{4}$��k2=-$\frac{3}{2}$��
��ֱ��AC�Ľ���ʽΪy=$\frac{3}{4}$x-3��ֱ��BC�Ľ���ʽΪy=-$\frac{3}{2}$x-3��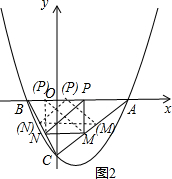
������ڣ���M��m��$\frac{3}{4}$m-3����0��m��4������N��-$\frac{1}{2}$m��$\frac{3}{4}$m-3����
��PMNΪ����ֱ�������η������������ͼ2��ʾ����
�ٵ���OMN=90��ʱ��P��m��0����
�ߡ�PMNΪ����ֱ�������Σ�
��$\frac{3}{4}$m-3=-$\frac{1}{2}$m-m����ã�m=$\frac{4}{3}$��
��ʱ��P������Ϊ��$\frac{4}{3}$��0����
�ڵ���PNM=90��ʱ��P��-$\frac{1}{2}$��0����
�ߡ�PMNΪ����ֱ�������Σ�
��$\frac{3}{4}$m-3=-$\frac{1}{2}$m-m����ã�m=$\frac{4}{3}$��
��ʱ��P������Ϊ��-$\frac{2}{3}$��0����
�۵���MPN=90��ʱ��P��$\frac{1}{4}$m��0����
�ߡ�PMNΪ����ֱ�������Σ�
��2����$\frac{3}{4}$m-3��=-$\frac{1}{2}$m-m����ã�m=2��
��ʱ��P������Ϊ��$\frac{1}{2}$��0����
���Ͽ�֪����x���ϴ��ڵ�P��ʹ�á�PMNΪ����ֱ�������Σ���P������Ϊ��$\frac{4}{3}$��0������-$\frac{2}{3}$��0����$\frac{1}{2}$��0����
���� ���⿼���˴���ϵ������������ʽ�������ε������ʽ�Լ�����ֱ�������ε����ʣ�����Ĺؼ��ǣ���1�����ö��κ����������ҳ���B�������Լ����������ε������ʽ���OC����2�����ô���ϵ���������������ʽ����3��������������ǣ����ݵ���ֱ�������ε������ҳ�����m��һԪһ�η��̣����������е��⣬�ѶȲ������������Ŀʱ�����ݵ���ֱ�������ε������ҳ�����M�ĺ�����ķ����ǹؼ���


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У������߾�������ԭ��O��x������һ��E������M������Ϊ��2��4��������ABCD�Ķ���A���O�غϣ���B��D������ֱ�Ϊ��0��3������-2��0����������ABCD��ÿ��1����λ���ȵ��ٶ���x���������ƽ�ƣ�ͬʱ��PҲ��ÿ��a����λ���ȴ�A��������A��B��C��D�˶�������Dֹͣ��������ƶ���ʱ��Ϊt��s����
��ͼ����ƽ��ֱ������ϵ�У������߾�������ԭ��O��x������һ��E������M������Ϊ��2��4��������ABCD�Ķ���A���O�غϣ���B��D������ֱ�Ϊ��0��3������-2��0����������ABCD��ÿ��1����λ���ȵ��ٶ���x���������ƽ�ƣ�ͬʱ��PҲ��ÿ��a����λ���ȴ�A��������A��B��C��D�˶�������Dֹͣ��������ƶ���ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ������ABCD�Ƶ�B��ʱ����ת30���õ�����A1BC1D1��C1D1��AD���ڵ�M���ӳ�DA��A1D1��F����AB=1��BC=$\sqrt{3}$����AF�ij���Ϊ��������
��ͼ������ABCD�Ƶ�B��ʱ����ת30���õ�����A1BC1D1��C1D1��AD���ڵ�M���ӳ�DA��A1D1��F����AB=1��BC=$\sqrt{3}$����AF�ij���Ϊ��������| A�� | 2-$\sqrt{3}$ | B�� | $\frac{\sqrt{3}-1}{3}$ | C�� | $\frac{3-\sqrt{3}}{3}$ | D�� | $\sqrt{3}$-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | AB=AC | B�� | AB��AC | C�� | ��B=��C | D�� | ��B�١�C |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �˽�һ���ڵ���ɱ�˰뾶 | |
| B�� | �˽�ȫ����ѧ����������� | |
| C�� | ���г���ij��������������ĵ��� | |
| D�� | ����һ������ս���ĸ��㲿����������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4 | B�� | 3 | C�� | 2 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com