
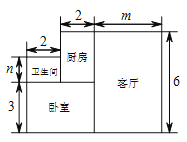
【题目】小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含 ![]() 的代数式表示地面的总面积
的代数式表示地面的总面积 ![]() ;
;
(2)已知 ![]() ,且客厅面积是卫生间面积的
,且客厅面积是卫生间面积的 ![]() 倍,如果铺
倍,如果铺 ![]() 平方米地砖的平均费用为
平方米地砖的平均费用为 ![]() 元,那么小王铺地砖的总费用为多少元?
元,那么小王铺地砖的总费用为多少元?
科目:初中数学 来源: 题型:
【题目】某工厂第一车间有x人,第二车间比第一车间人数的![]() 少20人,如果从第二车间调出15人到第一车间,那么
少20人,如果从第二车间调出15人到第一车间,那么
(1)调动后,第一车间的人数为 人;第二车间的人数为 人.
(2)调动后,第一车间的人数比第二车间的人数多多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某房地产开发商 2010 年 6 月从银行贷款 3 亿元开发某楼盘,贷款 期限为两年,贷款年利率为 8%.该楼盘有 A、B 两种户型共计 500 套房,算 上土地成本、建筑成本及销售成本,A 户型房平均每平方米成本为 0.6 万元,
B 户型房平均每平方米成本为 0.7 万元,表是开发商原定的销控表:
销售面积(m2) | 销售价格(万元/m2) | |
A 户型 | 75 | 0.8 |
B 户型 | 100 | 1 |
(1)该楼盘两种户型房各有多少套?
(2)由于限购政策的实施,2011 年以来房地产市场萎靡不振,开发商又急于在两年贷款期限到之前把房卖完,2012 年 1 月实际开盘时将 A 户型房按原定销 售价打 9 折,B 户型房按原定销售价打 8.3 折出售,结果 2012 年 6 月前将两 种户型的房全部卖完,开发商在还完贷款及贷款利息之后,还获利多少万元? 实际销售额比原定销售额下降了百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P1是一块半径为1的半圆形纸板,在P1的右上端剪去一个直径为1的半圆后得到图形P2,然后依次剪去一个更小的半圆(其直径为前一个被剪去的半圆的半径)得到图形P3、P4…Pn…,记纸板Pn的面积为Sn,则S2018-S2019的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中.过一点分別作坐标轴的垂线,若与坐标轴围成矩形的周长的数值与面积的数值相等,则这个点叫做和谐点.例如.图中过点P分別作x轴,y轴的垂线.与坐标轴围成矩形OAPB的周长的数值与面积的数值相等,则点P是和谐点.
(1)判断点M(1,2),N(4,4)是否为和谐点,并说明理由;
(2)若和谐点P(a,3)在直线y=﹣x+b(b为常数)上,求a,b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某校课外体育兴趣小组射击队日常训练中,教练为了掌握同学们一阶段以来的射击训练情况,对射击小组进行了射击测试,根据他们某次射击的测试数据绘制成不完整的条形统计图及扇形统计图如图所示:
(I)请补全条形统计图;
(II)填空:该射击小组共有____个同学,射击成绩的众数是_____,中位数是____;
(III)根据上述数据,小明同学说“平均成绩与中位数成绩相同”,试判断小明的说法是否正确?并说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是长方体纸盒的平面展开图,设 AB=x cm,若 AD =4x cm,AN=3x cm.
(1)求长方形 DEFG 的周长与长方形 ABMN 的周长(用字母 x 进行表示);
(2)若长方形 DEFG 的周长比长方形 ABMN 的周长少 8cm,求 x 的值;
(3)在第(2)问的条件下,求原长方体纸盒的容积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜宾市某化工厂,现有A种原料52千克,B种原料64千克,现用这些原料生产甲、乙两种产品共20件.已知生产1件甲种产品需要A种原料3千克,B种原料2千克;生产1件乙种产品需要A种原料2千克,B种原料4千克,则生产方案的种数为( )
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分类讨论是一种重要的数学方法,如在化简|a|时,可以这样分类:当a>0时,|a|=a;当a=0时,|a|=0;当a<0时,|a|=﹣a.用这种方法解决下列问题:
(1)当a=5时,求![]() 的值.
的值.
(2)当a=﹣2时,求![]() 的值.
的值.
(3)若有理数a不等于零,求![]() 的值.
的值.
(4)若有理数a、b均不等于零,试求![]() +
+![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com