Question

3．已知矩形ABCD中，AB=$\sqrt{3}$，BC=3，将△ACD绕点C顺时针旋转得到△EFG，使点D的对应点G落在BC延长线上，点A对应点为E点，C点对应点为F点，F点与C点重合（如图1）此时将△EFG以每秒2个单位长度的速度沿直线CB向左平移，直至点G与点B重合时停止运动，设△EFG运动的时间为t（t≥0）
（1）当t为何值时，点D落在线段EF上？
（2）设在平移过程中△EFG与△ACD重叠部分的面积为S，请直接写出S与t之间的函数关系式，并写出相应的t的取值范围；
（3）在平移过程中，当点G与点B重合时，如图2，将△CBA绕点B旋转得到△C₁A₁B，直线EF与C₁A₁所在直线交于P点，与C₁B₁所在直线交于点Q，在旋转过程中，△ABC的旋转角为α（0＜α°＜90°），是否存在这样的α，使△C₁PQ为等腰三角形？若存在，请求出旋转方向及α的度数；若不存在，请说明理由．

Answer 1

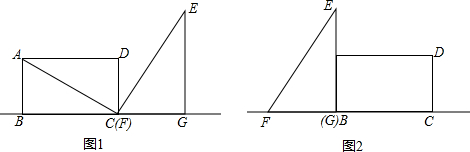
分析 （1）利用三角函数求出线段CD，延长AD交EF于点H，利用三角函数即可求出线段DH长度，再除以运动速度即为运动时间；
（2）根据勾股定理求出AB=$\sqrt{3}$，AC=4$\sqrt{3}$，即FG=$\sqrt{3}$，EG=2$\sqrt{3}$，再根据运动时间分五种情况进行讨论：①当 0＜t≤2时；②当2＜t≤2$\sqrt{3}$时；③当2$\sqrt{3}$＜t≤6时；④当6＜t≤8时；⑤当8＜t＜6+2$\sqrt{3}$时；根据三角形的面积和长方形的面积求出重合面积，写出S关于t的函数关系式即可；
（3）通过分析△C₁PQ为等腰三角形，分析等腰情况，分别求出对应角度即可．

解答 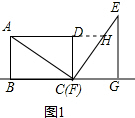解：（1）延长AD交EF于点H，如下图：
∵△ACD绕点C顺时针旋转得到△EFG，
∴∠DFH=30°，
∴DH=DF×tan30°=1，
∵△EFG以每秒2个单位长度的速度沿直线CB向左平移，1÷2=0.5秒，
∴当t=0.5时，点D落在线段EF上；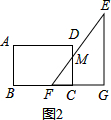

（2）∵矩形ABCD中，AB=$\sqrt{3}$，BC=3，
∴AB=$\sqrt{3}$，AC=2$\sqrt{3}$，
∴FG=$\sqrt{3}$，EF=2$\sqrt{3}$．
分五种情况进行讨论：
①当 0＜t≤2时，如图2，CF=t，CM=$\sqrt{3}$t，
则S=$\frac{1}{2}$CF•CM=$\frac{1}{2}$×t×$\sqrt{3}$t=$\frac{\sqrt{3}}{2}$t²；
②当2＜t≤2$\sqrt{3}$时，如图3，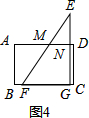
CF=t，CD=AB=2$\sqrt{3}$，
则DM=t-2，
∴S=$\frac{1}{2}$（DM+CF）•CD=$\frac{1}{2}$（t-2+t）×2$\sqrt{3}$=2$\sqrt{3}$t-2$\sqrt{3}$；
③当2$\sqrt{3}$＜t≤6时，如图4，FG=2$\sqrt{3}$，MN=$\frac{\sqrt{3}}{3}$DE=$\frac{\sqrt{3}}{3}$（6-2$\sqrt{3}$）=2$\sqrt{3}$-2，
∴S=$\frac{1}{2}$（MN+FG）•CD=$\frac{1}{2}$×（2$\sqrt{3}$-2+2$\sqrt{3}$）×2$\sqrt{3}$=12-2$\sqrt{3}$；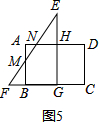
④当6＜t≤8时，如图5，BG=FG-BF=2$\sqrt{3}$-（t-6）=2$\sqrt{3}$+6-t，AN=BG-NH=（2$\sqrt{3}$+6-t）-（2$\sqrt{3}$-2）=8-t，
∴AM=$\sqrt{3}$AN=8$\sqrt{3}$-$\sqrt{3}$t，
∴S=S_矩形ABGH-S_△AMN=-$\frac{\sqrt{3}}{2}$t²+6$\sqrt{3}$t-20$\sqrt{3}$+12；
⑤当8＜t＜6+2$\sqrt{3}$时，如图6，BG=2$\sqrt{3}$+6-t，
∴S=BG•AB=-2$\sqrt{3}$t+12$\sqrt{3}$+12；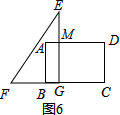

（3）∵△C₁PQ为等腰三角形，
当PQ=PC′，如下图7：
则∠Q=∠C′=30°，
∴∠EPC′=60°，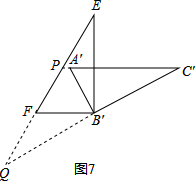
∵∠E=30°，
∴∠A′B′E=30°，
∴α=30°．
同理：当PQ=QC′，PC′=QC′，α=120°、165°．
∴△C₁PQ为等腰三角形，旋转角为30°、120°、165°．

点评 此题属于几何变换综合题．考查了旋转的性质、平移的性质以及等腰三角形的性质等知识．解决此类问题的关键分析图形的变换情况，在变换过程中，找准变量和不变量．