

分析 (1)设抛物线为y=a(x-1)2+3,当抛物线经过A(2,0)或(6,0)时求出a的值即可确定a的范围.
(2)根据条件可以知道F(1-8a,2)代入设抛物线为y=a(x-1)2+3即可求出a.
(3)作点B关于直线CQ的对称点B′,点B关于直线CP的对称点B″,连接B′B″分别交CQ、CP于点M、N,此时BM+MN+BN最小,通过证明这个最小值是定值为4,然后证明△BMN是直角三角形,题目转化为求周长为4的直角三角形的面积的最大值了,利用不等式的性质可以解决.
解答 解:(1)∵抛物线y=ax2+bx+c的顶点D(1,3),可以设抛物线为y=a(x-1)2+3,
当经过A(2,0)时,得到a=-3,
当经过A(6,0)时,得到a=-$\frac{3}{25}$,
∴-3≤a≤-$\frac{3}{25}$.
(2)∵△DEF的面积为-8a,且EF到x轴的距离等于2,
∴$\frac{1}{2}$•EF•1=-8a,
∴EF=-16a,
∴F(1-8a,2)代入抛物线为y=a(x-1)2+3,
∴2=64a3+3
a=-$\frac{1}{4}$,
∴抛物线为y=-$\frac{1}{4}$(x-1)2+3.
(3)存在.
如图作点B关于直线CQ的对称点B′,点B关于直线CP的对称点B″,连接B′B″分别交CQ、CP于点M、N.
此时BM+MN+BN最小,
∵∠MCB=∠MCB′,∠NCB=∠NCB″,CB=CB′=CB″=2$\sqrt{2}$,NB=NB″,MB=MB′,
∴∠B′CB″=2∠MCN=2×45°=90°,B′B″=$\sqrt{2}$CB′=4,
∴BM+NB+MN的最小值=4.
∵∠B′=∠B″=45°,
∴∠CBM=∠CBN=45°,
∴∠MBN=90°,
∴MN2=BM2+BN2,MN+BM+BN=4,
设BM=a,BN=b,MN=c,
∵a+b+c=4,
∴a+b+$\sqrt{{a}^{2}+{b}^{2}}$=4,
∵a+b≥2$\sqrt{ab}$,a2+b2≥2ab,
∴2$\sqrt{ab}$+$\sqrt{2ab}$≤4,
∴$\sqrt{ab}$≤2(2-$\sqrt{2}$)
∴ab≤24-16$\sqrt{2}$,
∴$\frac{1}{2}$ab≤12-8$\sqrt{2}$,
∴由BM、MN、NB组成的三角形面积的最大值为12-8$\sqrt{2}$.
点评 本题考查二次函数、对称的性质、三角形的面积、最小值问题、勾股定理等知识,学会利用对称找到BM+MN+NB最小时的位置,利用不等式性质确定周长为定值的直角三角形面积的最大值,是这个题目的难点.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:解答题
| +15 | -3 | +14 | -11 | +10 | -12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
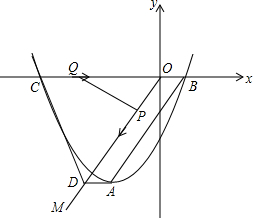 如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.
如图,顶点为A的抛物线y=a(x+2)2-4交x轴于点B(1,0),连接AB,过原点O作射线OM∥AB,过点A作AD∥x轴交OM于点D,点C为抛物线与x轴的另一个交点,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
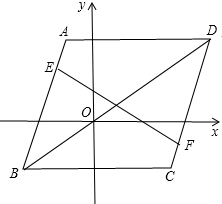 如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).
如图,在平面直角坐标系中,A(-1,3),B(-3,-2),C(3,-2),D(5,3),AB=CD,点E、F分别在AB、CD上,试判断∠BEF和∠DFE的大小关系并说明理由(提示:连接BD,先证明AB∥CD).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com