
 如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是$\frac{\sqrt{10}}{10}$.
如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是$\frac{\sqrt{10}}{10}$. 分析 利用勾股定理求出AB、AO、BO的长,再由S△ABO=$\frac{1}{2}$AB•h=$\frac{1}{2}$AO•BO•sin∠AOB可得答案.
解答 解:由题意可知,AB=2,AO=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,BO=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵S△ABO=$\frac{1}{2}$AB•h=$\frac{1}{2}$AO•BO•sin∠AOB,
∴$\frac{1}{2}$×2×2=$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{2}$×sin∠AOB,
∴sin∠AOB=$\frac{\sqrt{10}}{10}$,
故答案为:$\frac{{\sqrt{10}}}{10}$.
点评 本题主要考查锐角的三角函数,掌握三角形的面积公式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
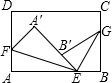 如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?
如图所示,将长方形纸片的角斜折.使顶点A落在A′处,EF为折痕,再将另一角斜折,使顶点B落在EA′上B′点处,折痕为EC,估计∠FEC的度数,你能说出理由吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com