
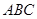 内接于⊙
内接于⊙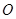 ,点
,点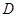 在
在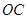 的延长线上,sinB=
的延长线上,sinB=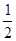 ,∠CAD=30°⑴求证:
,∠CAD=30°⑴求证: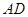 是⊙
是⊙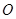 的切线;⑵若
的切线;⑵若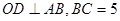 ,求
,求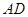 的长。
的长。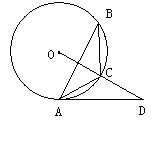
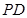 是⊙
是⊙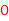 的切线
的切线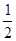 ∴∠B=30°∴∠AOC=60°.
∴∠B=30°∴∠AOC=60°.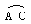 =
=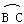 ∴AC=BC=5
∴AC=BC=5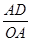 ,
, 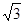 ……………8分
……………8分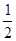 ,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;
,那么可求∠B=30°,利用圆周角定理可求∠AOC=60°,而OA=OB,那么△AOC是等边三角形,从而有∠OAC=60°,易求∠OAD=90°,即AD是⊙O的切线;

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源:不详 题型:填空题
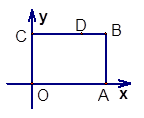
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
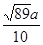 的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
的圆孔,需对铁片进行处理(规定铁片与圆孔有接触时铁片不能穿过圆孔);
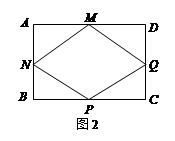

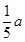 时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由;
时,判断直角梯形铁片EBAF能否穿过圆孔,并说明理由; 查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
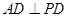 (2)若圆的半径为1,△ABE是等边三角形,求BP的长.
(2)若圆的半径为1,△ABE是等边三角形,求BP的长.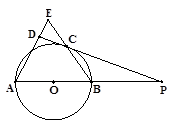
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
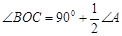 ;
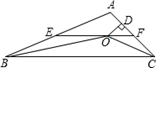
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com