
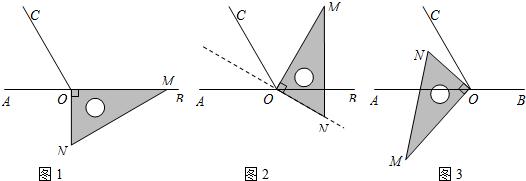
如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:3,将一直角△MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.绕点O顺时针旋转△MON,其中旋转的角度为α(0<α<360°).

(1)将图1中的直角△MON旋转至图2的位置,使得ON落在射线OB上,此时α为 度;

(2)将图1中的直角△MON旋转至图3的位置,使得ON在∠AOC的内部.试探究∠AOM
与∠NOC之间满足什么等量关系,并说明理由;
(3)在上述直角△MON从图1旋转到图3的位置的过程中,若直角△MON绕点O按每秒25°的速度顺时针旋转,当直角△MON的直角边ON所在直线恰好平分∠AOC时,求此时直角△MON绕点O的运动时间t的值.
(1)270(2)∠AOM-∠NOC=45°(3)t=4.5s或11.7s.
【解析】
试题分析:(1)270
(2)解:∠AOM-∠NOC=45°,∵∠AOC︰∠BOC=1︰3,∵∠AOC+∠BOC=180°,
∴∠AOC=45°,∠BOC=135°,∴∠1+∠2=45° ①
∵∠MON=90°,∴∠2+∠3=90° ②
由①②可得:∠3-∠1=45°,即∠AOM-∠NOC=45°.
(3)解:1°当ON平分∠AOC时,由(2)可知:∠AOC=45°,∴∠1+∠2=45°.
∵ON平分∠AOC,∴∠1=∠2=22.5°,∵∠MON=90°,∴∠2+∠3=90°,
∴∠3=67.5°,∴旋转角度为:180°-67.5°=112.5°,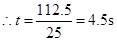 .
.
2°当ON的反向延长线平分∠AOC时.由(2)可知:∠AOC=45°.∴∠1+∠2=45°.
∵OE平分∠AOC,∴∠1=∠2=22.5°,∵∠MON=90°,∴∠3+∠4=90°.
∵∠3=∠2=22.5°,∴∠4=67.5°.
∴旋转角度为:360°-67.5°=292.5°.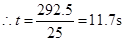 .∴t=4.5s或11.7s.
.∴t=4.5s或11.7s.
考点:中心旋转
点评:本题难度较大,主要考查学生对几何中心旋转知识点的掌握,综合运用几何性质与旋转性质解决问题的能力。为中考常考题型,要注意培养数形结合思想,运用到考试中去。


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 5 |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com