
|
|
| OF |
| EF |
| OA |
| CE |
| 1 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
|
|
| 3 |
| 4 |
| 3 |
| 4 |
|
|
|
| 15 |
| 4 |
| 33 |
| 16 |
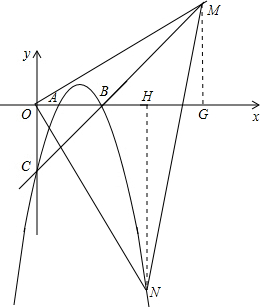 (3)在抛物线上存在点N(2,1)或(5,-8),能使三点O,M,N构成以O为直角顶点的等腰直角三角形.理由如下:
(3)在抛物线上存在点N(2,1)或(5,-8),能使三点O,M,N构成以O为直角顶点的等腰直角三角形.理由如下: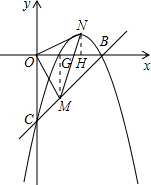 整理得:n2-n=0,故n=0或=1.
整理得:n2-n=0,故n=0或=1.

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
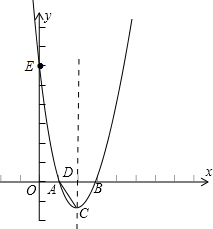 已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.
已知二次函数的图象是经过点A(1,0),B(3,0),E(0,6)三点的一条抛物线.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
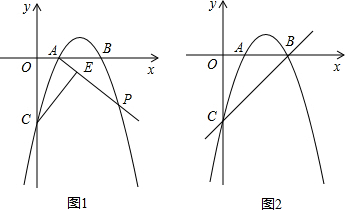
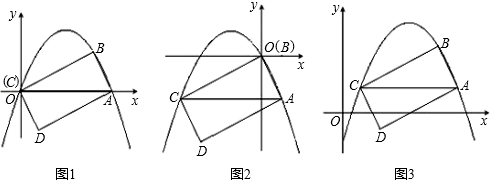
 阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
阅读材料:如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,将抛物线y=-
如图,将抛物线y=-| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com