
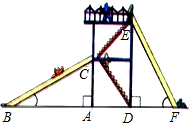
 如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.
如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.分析 (1)由图可得,△ABC与△DEF均是直角三角形,由已知可根据HL判定两三角形全等;
(2)利用(1)中全等三角形的对应角相等,可得∠ABC=∠DEF,再由∠DEF+∠DFE=90°利用等量代换可得∠ABC+∠DFE=90°.
解答 解:(1)△ABC与△DEF全等.
理由如下:
在Rt△ABC与Rt△DEF中,$\left\{\begin{array}{l}{BC=EF}\\{AC=DF}\end{array}\right.$,
∴Rt△ABC≌Rt△DEF(HL);
(2)∠ABC+∠DFE=90°,理由如下:
由(1)知,Rt△ABC≌Rt△DEF,则∠ABC=∠DEF,
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
点评 此题考查了全等三角形的判定及性质的运用.做题时要注意找已知条件,掌握全等三角形的判定方法.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 4cm,8cm | B. | 6cm,6cm | ||
| C. | 4cm,8cm或6cm,6cm | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 将一边长为3的等边三角形向右平移得到如图所示的图形,若阴影部分的面积为$\sqrt{3}$.现有一小孩向其投一小石子且已投中,则石子落在阴影部分的概率是( )
将一边长为3的等边三角形向右平移得到如图所示的图形,若阴影部分的面积为$\sqrt{3}$.现有一小孩向其投一小石子且已投中,则石子落在阴影部分的概率是( )| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{4}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com