
分析 ①根据分式的加法可以解答本题;
②根据分式的乘法和除法可以解答本题;
③根据分式的乘除法和加减法可以解答本题;
④根据分式的减法和除法可以解答本题.
解答 解:①$\frac{2a}{{a}^{2}-4}$+$\frac{1}{2-a}$
=$\frac{2a-(a+2)}{(a+2)(a-2)}$
=$\frac{a-2}{(a+2)(a-2)}$
=$\frac{1}{a+2}$;
②8m2n4•(-$\frac{3m}{4{n}^{3}}$)÷(-$\frac{{m}^{2}n}{2}$)
=8m2n4•(-$\frac{3m}{4{n}^{3}}$)×$(-\frac{2}{{m}^{2}n})$
=12m;
③($\frac{x}{x-y}$-$\frac{2y}{x-y}$)•$\frac{xy}{x-2y}$÷($\frac{1}{x}$+$\frac{1}{y}$)
=$\frac{x-2y}{x-y}•\frac{xy}{x-2y}•\frac{xy}{y+x}$
=$\frac{{x}^{2}{y}^{2}}{{x}^{2}-{y}^{2}}$;
④$\frac{a+1}{a-1}$-$\frac{a}{{a}^{2}-2a+1}$÷$\frac{1}{a}$
=$\frac{a+1}{a-1}-\frac{a}{(a-1)^{2}}•a$
=$\frac{{a}^{2}-1-{a}^{2}}{(a-1)^{2}}$
=$-\frac{1}{{a}^{2}-2a+1}$.
点评 本题考查分式的混合运算,解题的关键是明确分式的混合运算的计算方法.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个几何体由若干大小相同的小文体方块搭成,如图分别是从它的正面、上面看到的形状图.
一个几何体由若干大小相同的小文体方块搭成,如图分别是从它的正面、上面看到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
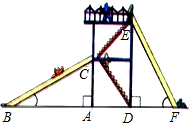 如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.
如图,幼儿园的滑梯有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在直线l3上,且不和点A,B重合.
如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在直线l3上,且不和点A,B重合.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com