

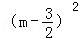 +
+ �������������� 6��
�������������� 6�� ��0��ʱ��PCmax=
��0��ʱ��PCmax= ����������������������������������������8��
����������������������������������������8��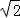 ��1+2
��1+2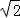 ����3+
����3+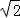 ��1��2
��1��2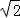 ����5����5����4��0����
����5����5����4��0����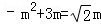 �����
�����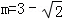 ��
��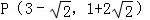 ��
�� ��
��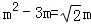 ��
��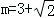 ��
�� ��
��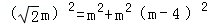 ��
��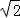 ��1+2
��1+2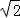 ����3+
����3+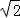 ��1��2
��1��2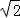 ����5����5����4��0����
����5����5����4��0����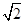 m����Ϊ����������ٵ�OC=PCʱ��m2-3m=
m����Ϊ����������ٵ�OC=PCʱ��m2-3m=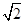 m��������̵Ľ⼴�ɵõ�P�����ꣻͬ�����ڵ�OC=OPʱ���۵�PC=OPʱ����P�����꣮�ۺ��������ɵõ��𰸣�
m��������̵Ľ⼴�ɵõ�P�����ꣻͬ�����ڵ�OC=OPʱ���۵�PC=OPʱ����P�����꣮�ۺ��������ɵõ��𰸣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������

 ������ֵy�����ֵ����Сֵ�����ֱ�ָ������Ӧ���Ա���x��ֵ��
������ֵy�����ֵ����Сֵ�����ֱ�ָ������Ӧ���Ա���x��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����ƽ��3����λ��������ƽ��4����λ���õ��������ߵĽ���ʽ�� ��
����ƽ��3����λ��������ƽ��4����λ���õ��������ߵĽ���ʽ�� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
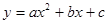 �Ķ���ΪP�������ߣ���y�ύ�ڵ�A����ֱ��OP���ڵ�B������P��PD��x���ڵ�D��ƽ��������Fʹ�侭����A��D�õ�������F�䣺
�Ķ���ΪP�������ߣ���y�ύ�ڵ�A����ֱ��OP���ڵ�B������P��PD��x���ڵ�D��ƽ��������Fʹ�侭����A��D�õ�������F�䣺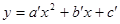 ��������F����x�����һ������ΪC��
��������F����x�����һ������ΪC��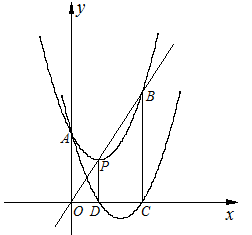
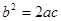
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A����2������ | B��2������ | C����1������ | D��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����ʽ����д�����Ķ������ꡢ�Գ���.
����ʽ����д�����Ķ������ꡢ�Գ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
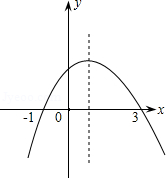
| A��1 | B��2 | C��3 | D��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 �Ķ�����x���ϣ��� b��ֵһ���ǣ� ��
�Ķ�����x���ϣ��� b��ֵһ���ǣ� ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
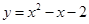 ��
�� ���һ������Ϊ
���һ������Ϊ �������ʽ
�������ʽ ��ֵΪ����
��ֵΪ����| A��2010 | B��2012 | C��2013 | D��2014 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com