

| MF2+MC2 |
| 2 |
| 1 |
| 2 |
| DG |
| AH |
| GH |
| AE |
| DG |
| 2 |
| 4 |
| x |
| 8 |
| x |
| 1 |
| 2 |
| 8 |
| x |
| 8 |
| x |
|
| AE |
| BC |
| AH |
| BE |
| x |
| 6 |
| 2 |
| 8-x |
| 20 |
| 3 |
| HA |
| AE |
| GD |
| DH |
| 2 |
| 2 |
| 2 |
| 2 |
| 20 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长,与BC的延长线交于点F,BD=BF.
如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长,与BC的延长线交于点F,BD=BF. |
| DE |
查看答案和解析>>
科目:初中数学 来源: 题型:
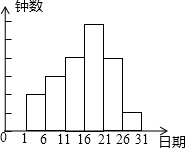 在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:
在学校开展的综合实践活动中,九(1)班进行了小制作评比,作品上交时间为5月1日到30日,评委会把同学们上交作品的件数按5天一组统计,绘制了频数分布直方图,如图所示,已知从左至右各小长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.
小明家今年种植樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行了跟踪记录,并将记录情况绘成图表.日销售量y(单位:kg)与上市时间x(单位:天)的函数关系如图所示,樱桃单价w(单位:元/kg)与上市时间x(单位:天)的函数关系列表所示,第1天到第a天的单价相同,第a天之后,单价下降,w与x之间是一次函数关系.| x(天) | 1 | a | 9 | 11 | 13 | … |
| w(元/kg) | 32 | 32 | 24 | 20 | 16 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:
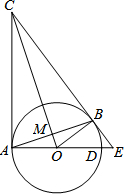 如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E. AB、CO交于点M,连接OB.| 1 |
| 2 |
| ||
| 10 |
| BE |
| AE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com